Varianza e deviazione standard

Per quantificare il concetto di incertezza di previsione riprendiamo l'esempio della distribuzione geometrica, che anche in questo caso si presta a confrontare il concetto intuitivo con la definizione operativa. Abbiamo visto che il valore atteso vale $1/p$ e che la variabile può assumere un qualsiasi valore intero positivo. Questo ci mostra che, se associassimo all'incertezza di previsione l'ampiezza dell'intervallo nel quale la variabile può verificarsi, questo sarebbe lo stesso (e per lo più di ampiezza infinita) per qualsiasi $p$. Ciò contrasta con l'idea intuitiva che la previsione del numero di prove per avere testa nel lancio di una moneta sia meno incerta del numero di settimane che bisogna attendere affinché esca un prefissato numero in una certa ruota del lotto.

Per arrivare alla definizione operativa, utilizziamo il concetto intuitivo secondo il quale se la previsione è ``buona'' (``poco incerta'') ci aspettiamo piccoli scarti fra il valore che si verificherà e la previsione stessa, ove per scarto intendiamo

$$\Delta = X -$$   E$$(X) = X-\mu\,.$$

Se invece la previsione è ``cattiva'' (``molto incerta'') ci aspettiamo grandi scarti. Quindi una possibile misura dell'incertezza di previsione potrebbe essere il valore atteso dei possibili scarti dalla previsione stessa^6.14, E$(X-\mu)$. Si può facilmente dimostrare come questa grandezza non sia adatta a misurare l'incertezza di previsione, essendo identicamente nulla per qualunque distribuzione:

E$$(X-\mu)=$$E$$(X)-\mu =0\,.$$

La ragione è dovuta al fatto che gli scarti positivi ($X-\mu>0$) sono compensati - in peso - da quelli negativi ($X-\mu<0$), anche se essi differiscono in numerosità (la distribuzione geometrica ne è un buon esempio).

Si potrebbe quindi provare con il valore atteso del modulo degli scarti. Tale quantità è in linea di principio accettabile, ma in pratica si preferisce il valore atteso del quadrato degli scarti perché, per dirla alla buona, è più comodo lavorare con i quadrati che con i moduli. Inoltre la quantità che ne risulta è - come vedremo fra breve - formalmente coniugata al valore atteso come il momento di inerzia lo è rispetto al baricentro. Infine, la grandezza risultante gode di proprietà generali molto interessanti e molto interessanti ai fini delle applicazioni (vedi paragrafo successivo e capitolo 10.)

Il valore atteso dei quadrati degli scarti è più spesso chiamato varianza ed è indicato dal simbolo $\sigma ^2(X)$ (o semplicemente $\sigma^2$ se non ci sono ambiguità):

$$\sigma ^2(X) \equiv (X) = [(X-\mu)^2]\,.$$ (6.33)

Come si vede dalla definizione, la varianza è pari alla media dei quadrati degli scarti, ciascuno pesato con la probabilità che ad esso si attribuisce (si ricorda che la probabilità di $\Delta=\delta_i=x_i-\mu$ è uguale a quella di $X=x_i$). Esplicitando l'operatore valore atteso otteniamo la seguente definizione operativa:

$$\sigma^2 = \sum_i(x_i-\mu)^2f(x_i)\,.$$ (6.34)

Dividendo il secondo membro per $\sum_i f(x_i)=1$, otteniamo

$$\sigma^2 = \frac{\sum_i(x_i-\mu)^2f(x_i)}{\sum_i f(x_i)}$$

dalla quale è evidente l'analogia meccanica con il momento di inerzia del sistema di punti ciascuno avente una ``massa di probabilità'' $f(x_i)$.

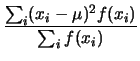Questa grandezza caratterizza la dispersione dei valori che possono verificarsi intorno a quello di previsione, ma ha l'inconveniente di non essere facilmente percepibile a livello intuitivo, non essendo omogenea alla previsione stessa. Si preferisce allora introdurre la deviazione standard, o scarto quadratico medio, definita come la radice quadrata (positiva) della varianza:

$$\sigma=\sqrt{\sigma^2}\,.$$ (6.35)

Quindi nel seguito associeremo il concetto qualitativo di "incertezza", quello operativo di incertezza standard, legato alla deviazione standard della distribuzione di probabilità.

In conclusione, il modo di riassumere sinteticamente lo stato di incertezza su un numero aleatorio consisterà in una affermazione del tipo:

$$\, \pm\, \,,$$ (6.36)

o, in simboli:

$$X = (X) \pm \sigma(X)$$

Come è noto nella vita quotidiana, quello che spesso interessa non è tanto l'entità dell'incertezza di previsione, quanto il suo valore rapportato a quello della previsione stessa. Ad esempio un'incertezza di 10 cm è enorme se riferita alla lunghezza di tavolo, piccolissima se riferita alla distanza fra due specchi distanti 10 km. La qualità della previsione è quantificata quindi dall'incertezza relativa (spesso espressa come percentuale). Essa è quantificata dal coefficiente di variazione, definito come

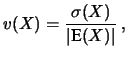$$v(X) = \frac{\sigma(X)}{\vert\mbox{E}(X)\vert}\,,$$ (6.37)

dove il modulo serve a poter utilizzare la stessa definizione indipendentemente dal segno della previsione.

A volte può essere opportuno aggiungere qualche altra grandezza che quantifichi in qualche modo convenzionale la forma della distribuzione, come può essere il grado di asimmetria fra le aspettative di scarti positivi rispetto a scarti negativi (vedi paragrafo 6.13).