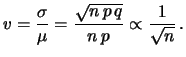Next: Usi tipici della distribuzione
Up: Proprietà della distribuzione binomiale
Previous: Proprietà della distribuzione binomiale
Indice
È abbastanza naturale pensare che
se si lancia 1000 volte una moneta ci si aspetta
un numero di teste intorno a 500.
Nello stesso modo è ovvio aspettarsi che se si
lancia un dado 20 volte si prevede che una certa faccia
uscirà circa un sesto del numero di lanci, anche se chiaramente
non potrà verificarsi 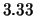 volte. Verifichiamo
come la definizione operativa di valore atteso sia in accordo
con tale previsione intuitiva:
volte. Verifichiamo
come la definizione operativa di valore atteso sia in accordo
con tale previsione intuitiva:
avendo chiamato, per comodità 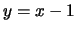 e utilizzando
le proprietà dei coefficienti binomiali
(vedi paragrafo 3.2.6).
e utilizzando
le proprietà dei coefficienti binomiali
(vedi paragrafo 3.2.6).
Per calcolare la varianza della distribuzione binomiale
è conveniente, come al solito, partire dal
valore atteso di 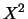 :
:
Da cui:
Nella seguente tabella riportiamo nel caso di lanci di una moneta i
valori attesi e la varianza del numero di teste.
 |
 |
 |
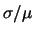 |
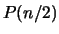 |
| 10 |
5 |
1.6 |
0.32 |
0.24 |
| 100 |
50 |
5.0 |
0.10 |
0.08 |
| 1000 |
500 |
16 |
0.032 |
0.025 |
| 10000 |
5000 |
50 |
0.010 |
0.010 |
| 1000000 |
500000 |
500 |
0.001 |
*** |
Si può osservare come al crescere di  ci attendiamo sempre
una maggiore dispersione di valori della variabile casuale
intorno al valore atteso7.1. In particolare,
si noti come al crescere di
ci attendiamo sempre
una maggiore dispersione di valori della variabile casuale
intorno al valore atteso7.1. In particolare,
si noti come al crescere di  il valore atteso diventi sempre meno probabile.
Diminuisce invece la dispersione relativa,
essendo il coefficiente di variazione pari a
il valore atteso diventi sempre meno probabile.
Diminuisce invece la dispersione relativa,
essendo il coefficiente di variazione pari a
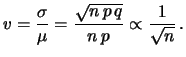 |
(7.7) |
Riassumendo, otteniamo che
la previsione dei valori della variabile
è uguale ad una frazione  del numero di prove da effettuare, con una
incertezza relativa di previsione inversamente proporzionale
alla radice quadrata del numero di prove.
del numero di prove da effettuare, con una
incertezza relativa di previsione inversamente proporzionale
alla radice quadrata del numero di prove.




Next: Usi tipici della distribuzione
Up: Proprietà della distribuzione binomiale
Previous: Proprietà della distribuzione binomiale
Indice
Giulio D'Agostini
2001-04-02
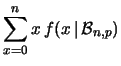
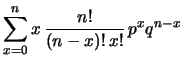
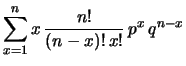
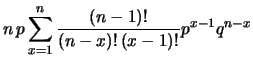
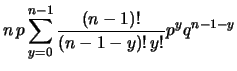
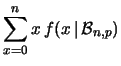
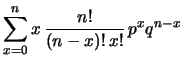
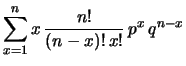
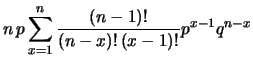
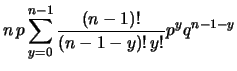
![]() :
:
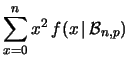
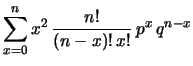
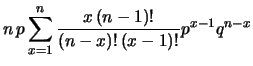
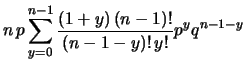
![]() ci attendiamo sempre
una maggiore dispersione di valori della variabile casuale
intorno al valore atteso7.1. In particolare,
si noti come al crescere di
ci attendiamo sempre
una maggiore dispersione di valori della variabile casuale
intorno al valore atteso7.1. In particolare,
si noti come al crescere di ![]() il valore atteso diventi sempre meno probabile.
Diminuisce invece la dispersione relativa,
essendo il coefficiente di variazione pari a
il valore atteso diventi sempre meno probabile.
Diminuisce invece la dispersione relativa,
essendo il coefficiente di variazione pari a