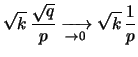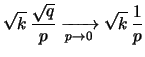Next: Distribuzione ipergeometrica
Up: pzd100 Altre distribuzioni di
Previous: Distribuzione di Pascal
Indice
Il problema precedente può essere trattato usando,
al posto
della variabile  precedente definita la variabile complementare
precedente definita la variabile complementare
 ``numero di insuccessi al momento in cui si verificano
esattamente
``numero di insuccessi al momento in cui si verificano
esattamente  successi'', ovvero
La distribuzione di probabilità di
successi'', ovvero
La distribuzione di probabilità di  si ricava direttamente
dalla (7.10):
si ricava direttamente
dalla (7.10):
Questa distribuzione è chiamata binomiale negativa
in quanto è possibile riscrivere la sua espressione
in modo da far comparire dei cosidetti coefficienti
binomiali negativi, scritti, in generale, come
formalmente analoghi dei normali coefficienti binomiali.
Per calcolare previsione e incertezza di previsione
si possono applicare direttamente le proprietà
degli operatori
E e
Var
e
Var alla trasformazione
alla trasformazione
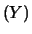 . Ne segue:
. Ne segue:
E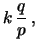 |
 |
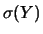 |
(7.16) |
Var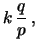 |
 |
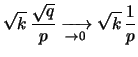 |
(7.17) |
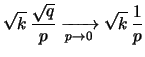 |
 |
![$\displaystyle \sqrt{k}\,\frac{\sqrt{q}}{p}
\xrightarrow[p\rightarrow 0]{}\sqrt{k}\,
\frac{1}{p}$](img1482.png) |
(7.18) |
 |
 |
![$\displaystyle \frac{1}{\sqrt{k\, q}}\xrightarrow[p\rightarrow 0]{}\frac{1}
{\sqrt{k}}\,.$](img1473.png) |
(7.19) |
Come ultima osservazione su questa distribuzione, che
non avremo più modo di incontrare nel seguito, è che
la sua complementarità con la distribuzione di Pascal
fa sì che sia possibile utilizzare la binomiale negativa
per risolvere dei problemi per la quale sarebbe più
naturale utilizzare quella. Inoltre, a volte in
alcuni testi è la
(7.15) ad essere
chiamata anche distribuzione di Pascal.
Si presti quindi attenzione.




Next: Distribuzione ipergeometrica
Up: pzd100 Altre distribuzioni di
Previous: Distribuzione di Pascal
Indice
Giulio D'Agostini
2001-04-02
![]() e
Var
e
Var![]() alla trasformazione
alla trasformazione
![]() . Ne segue:
. Ne segue: