Distribuzione ipergeometrica

Vediamo ora una distribuzione non legata al processo di Bernoulli, ma che rappresenta un modo alternativo per ottenere la distribuzione di binomiale.

Supponiamo che in una popolazione di $N$ persone ce ne siano $M$ una certa caratteristica. Se viene scelta una persona ``a caso'' la probabilità che essa abbia quella caratteristica è uguale a $p=M/N$. Se $n$ osservatori estraggono a caso ciascuno una persona, in modo che l'estrazione di un osservatore non sia influenzato da quella degli altri (e quindi la stessa persona può essere scelta più volte), la variabile casuale $X$ = ``numero di persone che presentano quella caratteristica'' ha probabilità secondo una binomiale di parametri $p$ e $n$.

***non si capisce *** Se invece vengono scelte contemporaneamente $n$ persone la variabile casuale $X$ ha diversa una distribuzione di probabilità. Ad esempio, nel caso limite in cui vengano prese tutte le $N$ persone, la variabile $X$ può assumere soltanto il valore $M$, e quindi non essa è più una variabile aleatoria, bensì un numero certo.

I due casi sono schematizzati con i classici problemi di estrazioni da urne di palline bianche e nere, con reintroduzione (o reimbussolamento) e senza reintroduzione. Nel primo caso vengono repristinate le condizioni iniziale dopo ogni estrazioni e quindi si ha la condizioni di indipendenza della probabilità che sta a base della distribuzione binomiale. Nel secondo caso la probabilità di estrarre, ad esempio, una pallina bianca dipende dal numero di palline bianche e nere estratte precedentemente.

Riformuliamo quindi il problema con lo schema dell'urna:

-

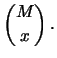un'urna contiene $N$ palline, di cui $M$ bianche e le $N-M$ restanti nere;

-

vengono estratte a caso e senza reintroduzione $n$ palline;

-

ci interessiamo alla variabile casuale $X$ = ``$x$ delle $n$ palline estratte sono bianche''.

Bisogna considerare i modi di scegliere $x$ palline bianche fra le $M$ totali, indipendentemente dal loro ordine. Essi sono dati dalle combinazioni semplici di $M$ elementi a gruppi di $x$:

$$\binom{M}{x}\,.$$

Per ciascuno di questi modi ci sono, con ragionamento analogo,

$$\binom{N-M}{n-x}$$

modi di estrarre le $n-x$ palline nere. Quindi il numero di casi favorevoli è dato dal prodotto dei due coefficienti binomiali.

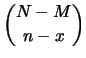Il numero dei casi possibili è dato dai numero di scelte di $n$ palline fra le $N$. Quindi, assumendo l'equiprobabilità, si ottiene

$$f(x\,\vert\,{\cal H}_{N,M,n}) = \frac{\binom{M}{x}\, \binom{N-M}{n-x}} {\binom{N}{n}}$$ (7.20)

$$= (0, n-(N-M)) \le x \le (n, M) \,.$$ con

Al di fuori di tali ovvii limiti la probabilità è pari a zero.

Questa distribuzione è chiamata distribuzione ipergeometrica. Diamo direttamente valore atteso e varianza:

$$(X) = n\,\frac{M}{N} = n\, r$$ (7.21)

$$(X) = n\,\frac{M}{N}\, \frac{N-M}{N}\, \frac{N-n}{N-1}$$

$$= n\, r \, (1-r) \frac{N-n}{N-1}$$ (7.22)

$$\sigma(X) = \sigma_B\sqrt{\frac{N-n}{N-1}}$$ (7.23)

ove con $r$ è stato indicato il rapporto fra il numero di palline bianche e il numero totale di palline e con $\sigma _B$ il prodotto $n\,r\,(1-r)$. Si noti che, se $n=N$, la varianza si annulla, in quanto diventa certo il solo esito $X=M$.

Tabella: Confronto fra alcune distribuzioni ipergeometriche e la binomiale aventi lo stesso numero di estrazioni ($n$) e con $r=p$ ($r$ indica $M/N$). Si noti il limite alla binomiale per $N\gg n$.

	Ipergeometrica per $n=4$ e $M=\frac{1}{2}N$				${\cal B}_{n=4,p=\frac{1}{2}}$
$x$	$N=4$	$N=6$	$N=10$	$N=100$
0	-	-	0.0238	0.0587	0.0625
1	-	$1/5=0.2$	0.2381	0.2499	0.2500
2	1	$3/5 =0.6$	0.4762	0.3827	0.3750
3	-	$1/5=0.2$	0.2381	0.2499	0.2500
4	-	-	0.0238	0.0587	0.0625
E$(X)$	2	2	2	2	2
$\sigma(X)$	0	0.63	0.82	0.98	1.00

Se $N$ è molto più grande di $n$, l'estrazione non cambia di molto le proporzioni di palline all'interno della scatola. Quindi ci si aspetta che quando $N/n \rightarrow\infty$ la distribuzione ipergeometrica tenda alla binomiale di parametri $n$ e $p=r=M/N$. Questo è in effetti il caso, anche se non lo dimostriamo. È invece immediato vedere come valore atteso e varianza tendano rispettivamente a $n\, p$ e a $n\, p\, (1-p)$ (questa è la ragione del simbolo $\sigma _B$ nella (7.25)). La tabella 7.3 mostra alcune distribuzioni ipergeometriche di $M = N/2$ e $n=4$ confrontate con la binomiale di $n=4$ e $p=1/2$.