next up previous contents
Next: Quanto credere in ``''? Up: Distribuzioni di probabilità di Previous: Distribuzione ipergeometrica   Indice

pzd100Cammino casuale e problema della rovina del giocatore

Come applicazione della distribuzione binomiale, immaginiamo il sequente processo. Una persona lancia una moneta: se esce testa fa un passo avanti; se esce croce fa un passo indietro (vedi figura 7.5). Dove si troverà dopo $ n$ lanci?

Figura: Processo di Bernoulli nel dominio del tempo.
\begin{figure}\centering\epsfig{file=fig/dago71.eps,clip=,width=0.8\linewidth}\end{figure}

Questo esempio illustra un importante modello di fenomeni casuali, chiamato cammino (o marcia) casuale o (in inglese random walk). Con esso è possibile descrivere fenomeni interessanti di diffusione come il moto browniano e la combinazione degli errori di misura, e anche la distribuzione di velocità delle molecole.

Per simmetria, il valore atteso della posizione dopo ogni passo è pari a zero (punto iniziale). Siamo quindi interessati a calcolare la sola varianza. Notiamo che se chiamiamo con $ S$ la variabile casuale ``spostamento in avanti'', con $ X$ il ``numero di teste'' e con $ Y$ il ``numero di croci'', abbiamo che $ S = X - Y\,.$ Ma poiché $ Y=n-X$, abbiamo

$\displaystyle S$ $\displaystyle =$ $\displaystyle 2\,X -n$ (7.24)
E$\displaystyle (S)$ $\displaystyle =$ $\displaystyle 2\,$E$\displaystyle (X) - n = 0$ (7.25)
Var$\displaystyle (S)$ $\displaystyle =$ Var$\displaystyle (X) = \frac{n}{2}$ (7.26)
$\displaystyle \sigma(S)$ $\displaystyle =$ $\displaystyle \sqrt{\frac{n}{2}}\,.$ (7.27)

Quindi la deviazione standard cresce come la radice quadrata del numero di passi compiuti. Per ricavare la distribuzione di probabilità di $ S$, notiamo che $ P(S=s)$ è uguale a $ P(X = (s+n)/2)$. Essendo $ X$ distribuita secondo una binomiale, ne segue:
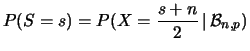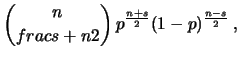$\displaystyle f(s)$ $\displaystyle \equiv$ $\displaystyle P(S=s) = P(X = \frac{s+n}{2}\,\vert\,{\cal B}_{n,p})$  
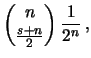  $\displaystyle =$ $\displaystyle \binom{n}{frac{s+n}{2}} \,p^{\frac{n+s}{2}}(1-p)^{\frac{n-s}{2}}\,,$ (7.28)

che nel nostro caso ($ p=1/2$) diventa
$\displaystyle f(s)$ $\displaystyle =$ $\displaystyle \binom{n}{\frac{s+n}{2}} \,\frac{1}{2^n}\,,$ (7.29)

La marcia a caso serve anche a descrivere un classico problema dei giochi d'azzardo, quello della rovina del giocatore. Per risolverlo si valuta la probabilità che un giocatore, iniziando a giocare con una certa somma iniziale $ s_\circ$, si trovi senza soldi ad un certo punto del gioco e quindi non possa più tentare la fortuna per rifarsi. In termini di marcia casuale è equivalente è equivalente a cominciare a $ s_\circ$ passi da un burrone. Per risolvere il problema, si parte dalle formule che abbiamo appena visto e si calcola la funzione di probabilità della variabile casuale $ K$ ``arriva in $ s_\circ$ allo spostamento $ k$'' (arrivare a $ s_\circ$ partendo da zero, è equivalente ad arrivare a zero partendo da $ s_\circ$).

Random walk, moto browniano ..

next up previous contents
Next: Quanto credere in ``''? Up: Distribuzioni di probabilità di Previous: Distribuzione ipergeometrica   Indice
Giulio D'Agostini 2001-04-02