



Next: Disuguaglianza di Markov
Up: Quanto credere in ``''?
Previous: Quanto credere in ``''?
Indice
La tabella 7.4 mostra, per alcuni
esempi di distribuzioni, i valori di probabilità legati agli
intervalli
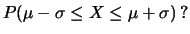 e
e
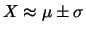 . Si noti che, trattandosi
di distribuzioni discrete definite per valori interi ed essendo
invece
. Si noti che, trattandosi
di distribuzioni discrete definite per valori interi ed essendo
invece  e
e  reali, potrebbe succedere per puro caso che,
a seconda dei parametri, l'intervallo
reali, potrebbe succedere per puro caso che,
a seconda dei parametri, l'intervallo
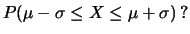 comprenda o no
uno o due valori della variabile, producendo una variazione discontinua nel
valore della probabilità. Siccome la tabella
7.4 è mostrata
a scopo indicativo,
gli intervalli sono stati arrotondati ai valori interi.
comprenda o no
uno o due valori della variabile, producendo una variazione discontinua nel
valore della probabilità. Siccome la tabella
7.4 è mostrata
a scopo indicativo,
gli intervalli sono stati arrotondati ai valori interi.
Tabella:
Probabilità che il numero aleatorio  sia compreso
nell'intervallo di una o due
sia compreso
nell'intervallo di una o due  intorno alla sua previsione,
valutata per alcune distribuzioni di probabilità.
intorno alla sua previsione,
valutata per alcune distribuzioni di probabilità.
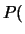 ``
``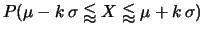 ''
''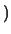 sta per
sta per
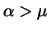 , dove
``
, dove
``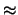 '' indica che le valutazioni sono in genere approssimate
arrotondando le ampiezze degli intervalli a valori interi.
Nell'ultima riga (``Cebicev'') è anche riportato il limite
ottenuto dall'uguaglianza di Cebicev
(vedi paragrafo 7.10.3).
'' indica che le valutazioni sono in genere approssimate
arrotondando le ampiezze degli intervalli a valori interi.
Nell'ultima riga (``Cebicev'') è anche riportato il limite
ottenuto dall'uguaglianza di Cebicev
(vedi paragrafo 7.10.3).
| |
|
|
|
|
| distr. |
 |
 |
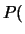 `` ``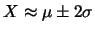 '' ''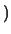 |
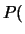 `` ``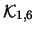 '' ''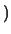 |
| |
|
|
(%) |
(%) |
| |
|
|
|
|
| |
|
|
|
|
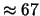 |
3.5 |
1.7 |
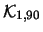 |
100 |
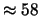 |
45.5 |
26 |
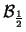 |
100 |
| |
|
|
|
|
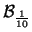 |
0.5 |
0.5 |
1 |
1 |
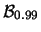 |
0.1 |
0.3 |
90 |
90 |
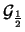 |
0.99 |
0.10 |
99 |
99 |
| |
|
|
|
|
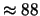 |
2.0 |
1.4 |
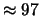 |
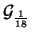 |
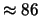 |
18.0 |
17.5 |
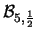 |
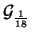 |
| |
|
|
|
|
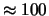 |
2.5 |
1.1 |
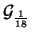 |
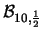 |
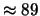 |
5.0 |
1.6 |
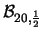 |
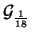 |
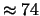 |
10.0 |
2.2 |
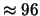 |
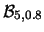 |
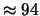 |
4.0 |
0.9 |
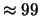 |
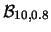 |
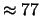 |
8.0 |
1.3 |
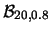 |
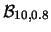 |
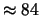 |
16.0 |
1.8 |
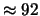 |
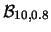 |
| |
|
|
|
|
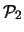 |
1.0 |
1 |
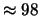 |
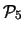 |
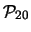 |
5.0 |
2.2 |
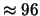 |
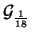 |
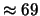 |
20.0 |
4.5 |
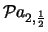 |
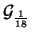 |
| |
|
|
|
|
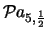 |
4.0 |
2.0 |
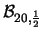 |
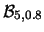 |
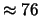 |
10.0 |
3.2 |
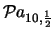 |
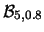 |
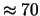 |
20.0 |
4.5 |
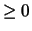 |
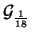 |
| |
|
|
|
|
| ``Cebicev'' |
- |
- |
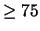 |
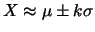 |
| |
|
|
|
|
|
Si noti come, nonostante le variazione da caso a caso,
si possa tranquillamente affermare che c'è ``buona'' probabilità
di trovare la variabile casuale ``entro un sigma''
dal valore atteso, mentre si è abbastanza sicuri che questo
si verifichi se si sceglie un ``intervallo di due sigma''.
Cosa si può dire invece su tale probabilità si conoscono
soltanto
i valori si 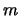 e
e  , ma non è dato di sapere il
tipo di distribuzione? Poiché valore atteso e varianza
sono legati alla distribuzione, ovvero, per dirlo in modo figurato,
alla configurazione dei valori della variabile casuale, in qualche modo
dovrebbe essere possibile affermare qualcosa di generale
su tale configurazione, che si rifletta sui valori di
probabilità di interesse. Questo è quanto affermato
dalla disuguaglianza di Cebicev,
dimostrata a partire dalla disuguaglianza di Markov
, ma non è dato di sapere il
tipo di distribuzione? Poiché valore atteso e varianza
sono legati alla distribuzione, ovvero, per dirlo in modo figurato,
alla configurazione dei valori della variabile casuale, in qualche modo
dovrebbe essere possibile affermare qualcosa di generale
su tale configurazione, che si rifletta sui valori di
probabilità di interesse. Questo è quanto affermato
dalla disuguaglianza di Cebicev,
dimostrata a partire dalla disuguaglianza di Markov




Next: Disuguaglianza di Markov
Up: Quanto credere in ``''?
Previous: Quanto credere in ``''?
Indice
Giulio D'Agostini
2001-04-02
![]() e
e ![]() , ma non è dato di sapere il
tipo di distribuzione? Poiché valore atteso e varianza
sono legati alla distribuzione, ovvero, per dirlo in modo figurato,
alla configurazione dei valori della variabile casuale, in qualche modo
dovrebbe essere possibile affermare qualcosa di generale
su tale configurazione, che si rifletta sui valori di
probabilità di interesse. Questo è quanto affermato
dalla disuguaglianza di Cebicev,
dimostrata a partire dalla disuguaglianza di Markov
, ma non è dato di sapere il
tipo di distribuzione? Poiché valore atteso e varianza
sono legati alla distribuzione, ovvero, per dirlo in modo figurato,
alla configurazione dei valori della variabile casuale, in qualche modo
dovrebbe essere possibile affermare qualcosa di generale
su tale configurazione, che si rifletta sui valori di
probabilità di interesse. Questo è quanto affermato
dalla disuguaglianza di Cebicev,
dimostrata a partire dalla disuguaglianza di Markov