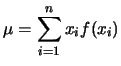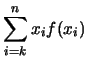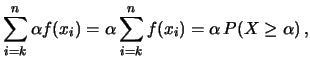Next: Disuguaglianza di Cebicev
Up: Quanto credere in ``''?
Previous: Alcuni esempi numerici
Indice
Questa disuguaglianza permette di stabilire un limite superiore
al valore di probabilità dalla sola conoscenza
del valore atteso  , a condizione che la variabile
casuale sia definita non negativa.
Dato un valore valore
, a condizione che la variabile
casuale sia definita non negativa.
Dato un valore valore
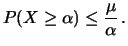 si ha che
si ha che
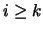 |
(7.30) |
Difatti, dalla definizione operativa di valore atteso e
scegliendo un valore di  tale che
per
tale che
per 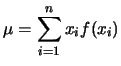
 sia maggiore di
sia maggiore di 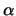 , segue
, segue
da cui segue la (7.32).
Per esempio, la sola conoscenza di 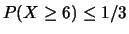 implica
implica
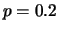 . Se però si venisse a sapere
che la distribuzione è di Poisson il valore di probabilità
sarebbe dell'1.7%; se fosse una binomiale di
. Se però si venisse a sapere
che la distribuzione è di Poisson il valore di probabilità
sarebbe dell'1.7%; se fosse una binomiale di 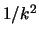 esso varrebbe 0.7; se una geometrica 1.6%. Tutti i valori sono compresi
entro il limite dato dalla (7.32).
esso varrebbe 0.7; se una geometrica 1.6%. Tutti i valori sono compresi
entro il limite dato dalla (7.32).




Next: Disuguaglianza di Cebicev
Up: Quanto credere in ``''?
Previous: Alcuni esempi numerici
Indice
Giulio D'Agostini
2001-04-02