Disuguaglianza di Cebicev

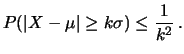La disuguaglianza di Cebicev afferma che la probabilità che lo scarto fra il valore della variabile casuale e la previsione di essa ecceda (o sia uguale) in modulo $k$ volte $\sigma$ non è maggiore di $1/k^2$ (con $k\ge 1$) . In formule:

$$P(\vert X-\mu\vert\ge k\sigma)\le \frac{1}{k^2}\,.$$ (7.31)

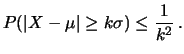Difatti il quadrato dello scarto $Y=(X-\mu)^2$ è una variabile casuale non negativa, che - per definizione di varianza - ha valore atteso $\mu_Y=\sigma^2$. Scegliendo un valore $\alpha = (k\,\sigma)^2$, con $k\ge 1$ in modo tale che $\alpha\ge\sigma^2$, possiamo applicare la disuguaglianza ad $Y$ di Markov:

$$P(Y \ge \alpha) \le \frac{\mu_Y}{\alpha}$$

$$P((X-\mu)^2 \ge (k\,\sigma)^2) \le \frac{\sigma^2}{(k\,\sigma)^2},$$

da cui segue la (7.33) in quanto $(X-\mu)^2 \ge (k\,\sigma)^2$ è equivalente a $\vert X-\mu\vert\ge k\sigma$.

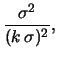Queste disuguaglianze sono di scarso valore pratico, in quanto è veramente raro il caso di non sapere assolutamente niente sul tipo di distribuzione, e la regola normativa della scommessa coerente che sta dietro le affermazioni di probabilità richiede di prendere in considerazione ogni informazione sugli eventi (invece di accontentarsi soltanto dei limiti ``di sicurezza''). Le utilizzazioni della disuguaglianza sono più di carattere teorico che applicativo. Infatti, è raro essere nelle condizioni di conoscenza per le quali vale tale teorema. Invece, le disuguaglinze permettono di dimostrare dei teoremi limite in modo indipendente dalla distribuzione di probabilità (vedi ad esempio paragrafo 10.9.2).

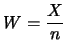Come esempio, riprendiamo quello già visto per illustrare la disuguaglianza di Markov. L'ulteriore conoscenza di $\sigma = 1.4$ (quanto si avrebbe per ${\cal P}_{2}$ o ${\cal G}_{\frac{1}{2}}$) o 1.3 (il caso di ${\cal B}_{10,0.2}$) modifica la probabilità di $P(X\ge 6)$ rispettivamente in $\le 12.3\,\%$ e $\le 10.6\,\%$, limiti meno laschi di quelli ottenuti dalla disuguaglianza precedente, ma ancora lontani dai valori che l'esatta conoscenza delle distrubuzioni forniscono.