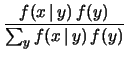Next: Ricapitolando
Up: Distribuzioni di probabilità di
Previous: Previsione della distribuzione statistica
Indice
 Estensione dei teoremi
sulla probabilità alle funzioni di probabilità
discrete
Estensione dei teoremi
sulla probabilità alle funzioni di probabilità
discrete
Avendo la funzione di probabilità di variabili casuali
discrete il significato di probabilità, si possono
applicare ad esse tutte le proprietà delle probabilità
incontrate nel capitolo
chap:RegoleProb. Basta
sostituire al simbolo 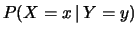 il simbolo
il simbolo 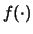 e ai generici eventi
e ai generici eventi 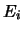 i valori assunti dalle variabili casuali.
Ad esempio,
i valori assunti dalle variabili casuali.
Ad esempio,
e così via.
In particolare l'ultimo esempio mostra come si costruisce
una variabile doppia, argomento sul quale ritorneremo
nel capitolo 9 (non perché
entrino in gioco concetti particolari, ma solo per seguire
un certo ordine di esposizione del matriale).
Vediamo ora come si estende
il teorema di Bayes,
facendo degli esempi di inferenza che ci serviranno di preparazione ai
problemi di inferenza sui valori di grandezze fisiche.
Se abbiamo due variabili casuali  e
e  , la probabilità
che
, la probabilità
che  assuma il valore
assuma il valore 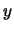 , subordinatamente all'informazione
che
, subordinatamente all'informazione
che  assuma il valore
assuma il valore  è data da:
è data da:
In termini di funzioni di probabilità
essa può essere scritta come
che, opportunamente normalizzata, diventa
Questa è l'espressione del teorema di Bayes per variabili
casuali discrete.
Tabella:
Sommario delle varie distribuzioni incontrate,
con relativi valori attesi e deviazioni standard. In genere, 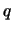 sta per
sta per 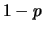 . Nella ipergeometrica
. Nella ipergeometrica  sta per
sta per 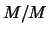 e
``
e
``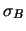 '' sta per la deviazione standard della binomiale
di
'' sta per la deviazione standard della binomiale
di 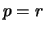 e stesso
e stesso  .
Per i domini
delle funzioni e il tipo di parametri si rimanda al testo.
.
Per i domini
delle funzioni e il tipo di parametri si rimanda al testo.
|
|
|
|
|
|
|
nome |
simbolo |
funzione |
 |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
uniforme |
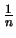 |
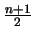 |
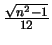
|
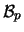 |
|
|
|
|
|
|
|
Bernoulli |
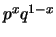 |
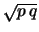 |

|
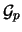 |
|
|
|
|
|
|
|
geometrica |
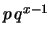 |
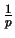 |
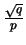
|
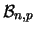 |
|
|
|
|
|
|
|
binomiale |
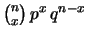 |
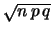 |
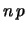 |
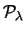 |
|
|
|
|
|
|
|
Poisson |
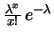 |
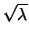
|
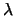 |
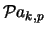 |
|
|
|
|
|
|
|
Pascal |
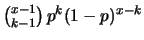 |
 |
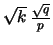 |
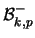 |
|
|
|
|
|
|
|
binomiale |
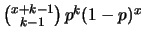 |
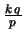 |
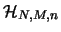 |
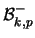 |
|
negativa |
|
|
|
|
|
|
|
|
|
|
|
ipergeometrica |
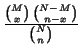 |
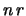 |
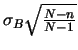
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|




Next: Ricapitolando
Up: Distribuzioni di probabilità di
Previous: Previsione della distribuzione statistica
Indice
Giulio D'Agostini
2001-04-02
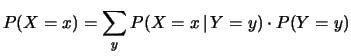
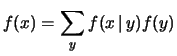
![]() e
e ![]() , la probabilità
che
, la probabilità
che ![]() assuma il valore
assuma il valore ![]() , subordinatamente all'informazione
che
, subordinatamente all'informazione
che ![]() assuma il valore
assuma il valore ![]() è data da:
è data da: