



Next: Distribuzioni di probabilità di
Up: Distribuzioni di probabilità di
Previous: Ricapitolando
Indice
- La Ferrero dichiara che 1 ovetto Kinder su 5 contiene una
sorpresa ``interessante''.
Un bambino compra 6 ovetti. Quanto vale la probabilità
che trovi esattamente 2 sorprese? Che ce ne trovi
almeno una?
- Seguito del problema precedente:
8 bambini acquistano ciascuno 6 ovetti. Quanto vale la
probabilità che esattamente 3 bambini trovino due sorprese?
- Sempre sui problemi precedenti: un bambino acquista
ogni giorno, mentre
va a scuola, due ovetti. Calcolare la previsione di
giorni che devono passare affinché gli capiti di vincere
due sorprese la stessa mattina.
- Una variabile casuale
 segue una distribuzione binomiale
di valor medio 4 e varianza 3. Trovare la probabilità che
la variabile casuale assuma un valore minore di 5.
segue una distribuzione binomiale
di valor medio 4 e varianza 3. Trovare la probabilità che
la variabile casuale assuma un valore minore di 5.
- Un esperimento consiste in 2 lanci di 5 monete diverse, lanciate
simultaneamente. Le monete sono: 100 Lit, 500 Lit, 1 DM, 1 FS
e 10 FF. Quante vale la probabilità che
in totale si verifichino esattamente
3 teste?
- Due monete vengono saldate fra di loro
in modo tale che risultino affiancate e che la testa dell'una
sia dalla stessa parte della croce dell'altra. Le due monete
sono lanciate per cinque volte. Quanto vale la probabilità di
osservare in totale esattamente 3 teste?
- Un esperimento consiste in: lancio di una moneta, lancio
di un dado, estrazione di un numero della tombola,
estrazione di un numero alla roulette ed estrazione di una carta
da gioco da un mazzo di 40 carte. Si definisce evento favorevole
nei diversi giochi il verificarsi, rispettivamente, di:
testa; numero 6; numero maggiore di 30; numero 8; denari.
Quanto vale la probabilità di avere un numero totale di successi
minore o uguale ad 1? Quanto vale la probabilità di
ottenere 5 eventi favorevoli?
- Un ingegnere della motorizzazione sa per sua esperienza che
il
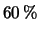 dei candidati riescano a passare
l'esame di guida.
Se in un giorno dovrà esaminare 10 candidati,
in quanto stimerà la probabilità che
almeno 8 siano promossi, senza nessun'altra informazione
(nemmeno guardandoli in faccia o sapendo età, sesso, etc.)?
dei candidati riescano a passare
l'esame di guida.
Se in un giorno dovrà esaminare 10 candidati,
in quanto stimerà la probabilità che
almeno 8 siano promossi, senza nessun'altra informazione
(nemmeno guardandoli in faccia o sapendo età, sesso, etc.)?
- Risolvere il problema sulla suddivisione della posta in caso
di interruzione del gioco (n. 31 del capitolo 2)
considerando la distribuzione
di probabilità del numero di vittorie dei due giocatori nelle
partite residue.
- Variazione sul tema del
problema delle sei scatole (nr. 18 e 19 del capitolo 5).
Immaginiamo che la scatola scelta sia stata preparata scegliendo
a caso 5 palline da un grande sacco che conteneva in
proporzione uguale palline bianche e nere.
Si calcoli
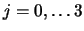 con
con
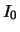 , ove
, ove 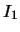 è
lo stato di informazione iniziale e
è
lo stato di informazione iniziale e 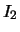 ,
, 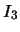 e
e 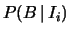 sono gli esiti delle estrazioni del problema 18 del capitolo 5.
Si calcoli anche
sono gli esiti delle estrazioni del problema 18 del capitolo 5.
Si calcoli anche
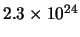 , ove
, ove  sta per la pallina bianca.
sta per la pallina bianca.
- In una razza di cani il mantello nero (
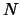 ) domina su quello
rosso (
) domina su quello
rosso ( ). Una cagna nera dal genotipo eterozigote (
). Una cagna nera dal genotipo eterozigote (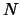 ,
,  )
viene incrociata con un maschio omozigote recessivo, ovvero (
)
viene incrociata con un maschio omozigote recessivo, ovvero ( ,
,  ).
Calcolare le probabilità che su 6 cuccioli ne nascano
rispettivamente 0, 1, 2, 3, 4, 5 e 6 di colore rosso.
).
Calcolare le probabilità che su 6 cuccioli ne nascano
rispettivamente 0, 1, 2, 3, 4, 5 e 6 di colore rosso.
- Un campione contiene
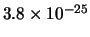 nuclei radioattivi.
La probabilità che uno dei nuclei possa
nell'intervallo di tempo di un secondo
vale
nuclei radioattivi.
La probabilità che uno dei nuclei possa
nell'intervallo di tempo di un secondo
vale
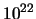 . Calcolare la probabilità di
registrare, durante un secondo di osservazione, un numero di
decadimenti pari a 0, 1, 2, 3, 4 e 5.
. Calcolare la probabilità di
registrare, durante un secondo di osservazione, un numero di
decadimenti pari a 0, 1, 2, 3, 4 e 5.
- È noto che un certi fenomeni si verificano casualmente
con una frequenza media di 50 l'ora. Calcolare la
probabilità di osservarne almeno uno in un intervallo
di osservazione di 30 secondi.
- Sul problema precedente. Ammettiamo di ripetere per
10 volte le osservazioni da 30 secondi precedentemente
descritte. Quanto vale la probabilità che in 5 delle
10 osservazioni non si verichi il fenomeno di interesse?
- Uno sperimentatore ha buoni ragioni per ritenere che il
numero di conteggi di un certo fenomeno segua la distribuzione
di Poisson. Valutare la probabilità che si verifichino
almeno 4 conteggi, sapendo che lo sperimenattore ritiene
che la probabilità
di non osservarne nessuno sia del 5%.
- Un campione di materia contiene
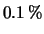 nuclei.
Un contatore di radioattività registra una frequenza
di decadimenti di 100 al minuto. Quanto vale la probabilità
che uno preciso nucleo decada in un intervallo di tempo
di un secondo?
nuclei.
Un contatore di radioattività registra una frequenza
di decadimenti di 100 al minuto. Quanto vale la probabilità
che uno preciso nucleo decada in un intervallo di tempo
di un secondo?
- Una dattilografa scrive un resoconto costituito da 15 cartelle.
Ciascuna cartella ha 20 linee di 60 caratteri ciascuna.
La probabilità che la dattilografa sbagli un carattere è
dello
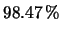 . Quanto vale la probabilità che in una cartella
non ci sia nemmeno un errore? Quanto vale la probabilità
che sull'intero resoconto ci siano al più 10 errori?
. Quanto vale la probabilità che in una cartella
non ci sia nemmeno un errore? Quanto vale la probabilità
che sull'intero resoconto ci siano al più 10 errori?
- Una variabile casuale segue una distribuzione di Poisson.
Sapendo che la probabilità che si verifichi un valore
diverso da 0 vale
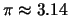 , determinare il coefficiente di
variazione della distribuzione.
, determinare il coefficiente di
variazione della distribuzione.
- Una variabile casuale segue una distribuzione
di Poisson. Sapendo che il valore medio della distribuzione
è pari a due volte il valore della deviazione standard,
trovare la probabilità che la variabile casuale assuma un valore
più grande di 2.
- Un certo giorno nel reparto di ostetria di un ospedale sono
disponibili
10 posti letto. La media giornaliera
del numero di donne che
si presentano al reparto per partorire è pari a 6.5.
Quanto vale la probabilità che una o più donne
possa essere non accettata?
- Fra le
16:00 e le 17:00
in un tratto di strada di una grande città transitano
in media 20 taxi. Il
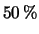 è occupato e, dei restanti,
il
è occupato e, dei restanti,
il 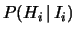 è prenotato. In base a queste informazioni:
è prenotato. In base a queste informazioni:
- Quanto vale la probabilità che un giorno passino al più 10 taxi
in quell'ora? E la probabilità che ne passino esattamente 10?
- Nel caso ne passino esattamente 10:
quanto vale la probabilità
che di essi almeno 2 siano liberi? E nel caso ne passano 20?
- Quanto vale la probabilità
che, uscendo dall'ufficio alle 16:30, si riesca a prendere un taxi al volo
entro un quarto d'ora?
- Quanto vale la
probabilità che in una settimana lavorativa di 5 giorni
si riesca almeno 2 volte a prendere un taxi entro un quarto d'ora?
- Uno strumento registra dei
di fenomeni casuali che seguono la distribuzione di Poisson e
si verificano con una frequenza di 50 volte al secondo.
Per quanto tempo bisognerà tenere lo strumento in funzione affinché
l'incertezza di previsione relativa sul numero di conteggi che
saranno registrati sia dell'1%?
- Riprendiamo il problema 9 del capitolo 2.
Supponiamo di disporre di un dispositivo (tipicamente un programma
di simulazione al computer) che permetta di distribuire in modo
casuale dei punti all'interno del quadrato. Supponiamo di generare
in totale 10000 punti. Trovare il valore atteso, la deviazione
standard e il coefficiente di variazione del numero di punti che
cade all'interno del quarto di cerchio. È possibile
utilizzare questo dispositivo per stimare empiricamante il
valore di
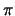 dalla frequenza osservata? Sapendo che
dalla frequenza osservata? Sapendo che
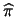 ,
quanti punti bisogna generare affinché
il coefficiente di variazione
di
,
quanti punti bisogna generare affinché
il coefficiente di variazione
di
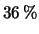 (``valore
misurato di
(``valore
misurato di 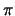 '')
sia pari a 0.0001?
'')
sia pari a 0.0001?
- Calcolare la previsione del numero di molecole in un
millimetro cubico di gas
perfetto a pressione atmosferica e ad una temperatura di
20
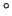 C.
C.
- Sui dati del problema precedente. Calcolare il lato
del cubo tale che sia del 10%la probabilità
che, ad un certo istante, non vi sia alcuna molecola al suo interno.
Per avere un'idea di quanto poco compatta sia la
materia in tali condizioni, stimare l'ordine di grandezza
del numero di molecole che sarebbe possibile compattare
all'interno di tale volumetto, assumendo per le molecole
delle dimensioni lineari dell'ordine di 0.1 nm.
- Un rivelatore risponde al passaggio di una particella emettendo
in media 1000 fotoni. In media l'
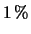 dei fotoni
riesce ad arrivare su un fotocatodo dove
ciascuno dei fotoni ha una
probabilità del
dei fotoni
riesce ad arrivare su un fotocatodo dove
ciascuno dei fotoni ha una
probabilità del 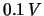 di emettere un elettrone. L'elettrone
entra in un dispositivo opportuno (fotomoltiplicatore)
che produce, con probabilità 1, un impulso elettrico
di ampiezza maggiore di
di emettere un elettrone. L'elettrone
entra in un dispositivo opportuno (fotomoltiplicatore)
che produce, con probabilità 1, un impulso elettrico
di ampiezza maggiore di 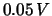 . Nel caso che, dal passaggio
di una particella siano prodotti più impulsi, questi vengono
sommati.
Infine, un dispositivo elettronico fornisce un segnale
percepibile dallo sperimentatore se esso riceve un impulso
di almeno
. Nel caso che, dal passaggio
di una particella siano prodotti più impulsi, questi vengono
sommati.
Infine, un dispositivo elettronico fornisce un segnale
percepibile dallo sperimentatore se esso riceve un impulso
di almeno 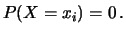 . Calcolare l'efficienza del rivelatore,
ovvero la probabilità che lo sperimentatore registri un
segnale al passaggio di una particella. (Assumere che
fra l'arrivo di due particelle passi abbastanza tempo
in modo tale che esse non diano luogo a segnali che si confonderebbero
fra di loro.)
. Calcolare l'efficienza del rivelatore,
ovvero la probabilità che lo sperimentatore registri un
segnale al passaggio di una particella. (Assumere che
fra l'arrivo di due particelle passi abbastanza tempo
in modo tale che esse non diano luogo a segnali che si confonderebbero
fra di loro.)
- Una persona fa il seguente solitario:
estrae a caso una carta da un mazzo da 52, la guarda e la rimette
nel mazzo, rimischia e cosi' via. Vince quando ha trovato
per 3 volte la regina dui cuori. Calcolare la previsione
(con relativa incertezza) del numero di volte che deve provare.
- In un paese il reddito medio per ogni persona è pari a 10000$
l'anno
con una deviazione standard di 3000$. Qual'è la probabilità
che scelta una persona a caso essa abbia
un reddito superiore a 30000$?
- Con riferimento ai dati sperimentali dei morti da calcio di
cavallo di tabella 7.6:
scelto a caso un ``ipotetico'' reggimento e scelti a caso due anni,
è giusto dire che
la probabilità che ci siano almeno due morti nel periodo dei
due anni sia il doppio della probabilità che ci sia almeno un morto
in un anno? La risposta dipende dal fatto che i due anni scelti
siano consecutivi o no?
- Sempre sugli stessi dati sperimentali del problema precedente:
immaginiamo di estrarre a sorte uno dei 200 reggimenti
che sono serviti a ricavare i dati di mortalità.
Quanto vale la probabilità che uno dei reggimenti registri
un numero di incidenti maggiore o uguale a 6?
- Risolvere il problema 10 del capitolo 4 facendo uso della distribuzione
ipergeometrica.
- Un insegnante vuole ``dimostrare'' che, lanciando un grande numero
di monete, la frequenza relativa di teste ``è'' del 50%.
Quante monete deve far lanciare dagli studenti affinché
la sua incertezza di previsione sia inferiore a 0.01?




Next: Distribuzioni di probabilità di
Up: Distribuzioni di probabilità di
Previous: Ricapitolando
Indice
Giulio D'Agostini
2001-04-02