Valutazione combinatoria

Assumiamo che l'esito di un possibile esperimento, ovvero l'evento di interesse, consista nella realizzazione di una tra più modalità elementari che si escludono a vicenda, ove con ``elementare'' si vuole indicare:

a)

l'impossibilità di classificare ulteriormente gli eventi in base a qualche caratteristica che hanno alcuni e non altri;

b)

che tali eventi devono essere tutti quelli possibili;

c)

che essi sono fra di loro a due a due incompatibili, ovvero che il verificarsi di uno escluda tutti gli altri.

Esempi di questi eventi sono le 6 faccie di un dado, i 90 numeri del lotto, e così via. Questi eventi sono spesso chiamati ``casi possibili'' e li indicheremo con il simbolo $e_i$. Ad esempio, per il lancio del dado, $e_1=\{1\}$, $e_2=\{2\}$, $\ldots$, $e_6=\{6\}$.

In generale più modalità elementari possono contribuire allo stesso evento. Ad esempio l'evento ``numero pari nel lancio del dado'' è costituito dai tre eventi elementari $e_2=\{2\}$, $e_4=\{4\}$ e $e_6=\{6\}$. Quenti eventi elementari vengono chiamati casi favorevoli e gli altri, di conseguenza, casi contrari.

Se il meccanismo di estrazione è talmente simmetrico rispetto a ciascuno dei casi possibili, nessuna modalità è da ritenersi più probabile delle altre. Questa osservazione è stata elevata a principio da Laplace. A tale principio fu successivamente dato il nome di Principio di Ragione non Sufficiente^2.1 o Principio di Indifferenza.

Per passare dalla equiprobabilità dei casi possibili alla valutazione numerica della probabilità rimane da definire una scala per i valori di probabilità. Per semplicità viene scelto il valore 0 per un evento impossibile e il valore 1 per un evento certo (anche se nella vita pratica si preferiscono le percentuali e si considera la probabilità compresa fra 0 e 100%).

Se $n$ è il numero di casi (ugualmente) possibili e $P(e_i)$ la probabilità di ciascun evento elementare, un evento generico $E_j$ che ha $n_j$ eventi favorevoli ha probabilità $n_j$ volte quella elementare. Poiché l'evento certo, di probabilità 1, è costituito da $n$ eventi elementari, ciascuno di questi ha probabilità $P(e_i)=1/n$, mentre per il generico evento vale $P(E_j)=n_j/n$.

Quindi, la probabilità di ciascuna delle modalità elementari, sotto condizione di equiprobabilità, è pari all'inverso del numero di casi possibili, mentre un generico evento ha probabilità proporzionale al numero delle modalità elementari nelle quali può manifestarsi. Da ciò segue la così detta ``definizione'' classica di Laplace :

il valore della probabilità di un dato evento è pari al rapporto tra il numero dei casi favorevoli all'evento e il numero dei casi possibili, se questi sono egualmente probabili:

$$p = \frac{\mbox{numero dei casi favorevoli}} {\mbox{numero dei casi egualmente\ probabili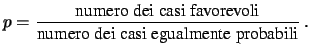}}\,.$$ (2.1)

Come si intuisce, questa ``definizione'' è utile per assegnare un numero al livello di probabilità, ma sicuramente non definisce la probabilità come concetto, in quanto essa si basa sul concetto primitivo di equiprobabilità. È altresì ovvio che tale definizione è soddisfatta in circostanze elementari facilmente schematizzabili, ma non è affatto adeguata a descrivere fenomeni complessi, che sono quelli di maggiore interesse per le applicazioni della vita reale. Ma, e soprattutto, è da notare come il giudizio di equiprobabilità sia lasciato a discrezione di chi valuta la probabilità, cioè esso è in larga misura ``soggettivo''.

A tale riguardo è istruttiva questa riflessione di Poincaré^2.2:

...Siamo costretti a definire il probabile dal probabile. Come possiamo sapere se due casi sono ugualmente probabili? Sarà per convenzione? Se inseriamo all'inizio di ogni problema una convenzione esplicita, bene! Allora non dobbiamo far altro che applicare le regole dell'aritmetica e dell'algebra e completare il calcolo, quando il nostro risultato non può essere chiamato in questione. Ma se vogliamo fare la minima applicazione di questo risultato dobbiamo provare che la nostra convenzione è legittima e ci troveremo in presenza della difficoltà di fondo che pensavamo di aver evitato.