Next: Legge empirica del caso Up: Valutazioni e interpretazioni della Previous: Valutazione combinatoria Indice

Probabilità e frequenza

Come accennato, il primo tentativo di valutare la probabilità fuori dall'ambito dei giochi d'azzardo fu motivato dal calcolo delle pensioni. L'ammontare del vitalizio da corrispondere all'assicurato dipende infatti, oltre che dal capitale accumulato e da altri fattori strettamente economici, dalla probabilità di morte dell'assicurato in funzione della sua età. Infatti, a seconda dei casi, la compagnia guadagna molto in caso di decesso prematuro, mentre perde molto nel caso di straordinaria longevità. Una valutazione realistica *** attenzione alle implicazioni di oggettività*** della probabilità è resa necessaria onde evitare perdite economiche nei casi di eccessive sottostime o sovrastime. Nel primo caso la società farà bancarotta a causa dei vitalizi troppo onerosi che si è impegnata a pagare, nel secondo sarà battuta dalla concorrenza che, disponendo di valutazioni più realistiche, potrà offrire ai clienti premi più convenienti.

Considerando la sopravvivenza di ciascuna persona da un anno all'altro, ci sono due modalità elementari, ma esse sono per fortuna non equiprobabili e quindi la ``definizione'' di Laplace è inapplicabile.

Il problema fu risolto compilando delle tabelle di mortalità per le varie età e stimando la probabilità dalla frequenza (ovvero da quante volte quel tipo di evento si è verificato nel passato).

Per essere più concreti - e meno macabri - interessiamoci ad esempio alla valutazione della probabilità di sopravvivenza nell'arco di un anno delle persone di una certa classe di età. Assumiamo che il $1^\circ$ di gennaio di un certo anno la popolazione sia costituita da individui di una certa età e che il $1^\circ$ gennaio dell'anno successivo siano ancora in vita di quegli . Questo era ritenuto equivalente ad aver compiuto esperimenti - o prove - dei quali hanno dato esito favorevole e esito sfavorevole. Ciascuna prova è inoltre considerata indipendente dall'altra e la probabilità di esito favorevole è ritenuta costante (è facile intuire come questa schematizzazione sia particolarmente rozza e che non potrà mai portare ad una valutazione della probabilità di sopravvivenza del singolo individuo, ma al più ad una probabilità relativa all'individuo tipo).

Nel valutare la probabilità di sopravvivenza dei nuovi individui che hanno ora raggiunto tale età si effettua il seguente ragionamento: in generale, se la valutazione di probabilità è corretta, l' esito a cui è assegnata probabilità più elevata è quello dei due che si ritiene possa accadere più facilmente. In particolare, se uno dei due fosse impossibile non accadrebbe mai, mentre se fosse certo si verificherebbe con sicurezza. Supponendo che il processo si ripeta nel futuro con le stesse condizioni con cui era avvenuto nel passato allora il ragionamento precedente può essere invertito (``l'esito più frequentemente accaduto è quello che ``aveva'' maggiore probabilità di accadere'') ed esteso al futuro ^2.3. La probabilità che i nuovi individui di quella classe di età sopravvivano è quindi ritenuta proporzionale al numero di eventi favorevoli () dell'anno precedente: $P(F)\propto n_f$ .

Poiché l'evento certo (``qualcosa deve accadere''), proporzionale a , viene convenzionalmente posto uguale ad 1, si ottiene che il fattore di proporzionalità vale . Ne segue che . Ovvero che la frequenza relativa di successo nel passato viene adottata a misura della probabilità di successo nel futuro.

Estendendo il semplice problema dell'esperimento con due esiti ad esperimenti a molti esiti, come potrebbe essere ad esempio quello di misure nelle quali il risultato si può presentare in tante modalità diverse (sia la -ma modalità), otteniamo

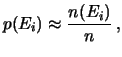$\displaystyle p(E_i) \approx \frac{n(E_i)}{n}\,,$

(2.2)

ovvero la probabilità viene valutata come

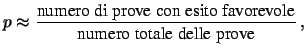$\displaystyle p \approx \frac{\mbox{numero di prove con esito favorevole}} {\mbox{numero totale delle prove}} \,,$

(2.3)

o, più concisamente,

$\displaystyle p$

$\displaystyle \approx$

frequenza relativa di successo $\displaystyle \,.$

Questo metodo di valutazione delle probabilità è affetto da due limitazioni:

innanzitutto il segno `` $\approx$ '' al posto di ``='' sta a ricordare che questa valutazione soffre di grosse incertezze se il numero di prove non è molto grande. Ad esempio, nel caso estremo in cui sia stata effettuata una sola prova, la frequenza relativa vale 0 o 1;
esso presuppone che gli esperimenti (passati, presenti e futuri) possano essere ripetuti nelle stesse condizioni, ovvero in modo indipendente l'uno dall'altro e con la probabilità di ciascuna delle modalità costante nella singola prova.

La prima limitazione può essere superata se si dispone di un grande numero di prove. La seconda invece è insita nella natura delle cose ed è compito di chi valuta la probabilità giudicare, di volta in volta, se l'ipotesi di equiprobabilità delle prove possa essere accettata entro i limiti di accuratezza con cui è necessario stimare la probabilità.

Quindi anche in questo caso spetta a chi valuta la probabilità decidere, con un ampio margine di arbitrarietà, se l'ipotesi di ``stesse condizioni'' è verificata e se le prove si svolgeranno nel futuro come si erano svolte nel passato. Ad esempio, se in una popolazione si sviluppa improvvisamente un'epidemia o se, al contrario, migliorate condizioni di vita e assenza di eventi bellici diminuiscono la mortalità non ci si può più basare sulle tabelle di sopravvivenza degli anni precedenti.

È da notare inoltre come la richiesta di un grande numero di prove possa essere in contrasto con la non - o scarsa - ripetibilità del fenomeno sotto studio. In genere sia lo strumento che la grandezza da misurare^2.4possono subire modificazioni nel corso del tempo. Che senso avrebbe, ad esempio, affermare che al 95% di probabilità una navicella spaziale si trova in un certo istante in una certa regione di spazio se si credesse che il solo modo di intendere la probabilità sia quello basato sulla frequenza?

Next: Legge empirica del caso Up: Valutazioni e interpretazioni della Previous: Valutazione combinatoria Indice

Giulio D'Agostini 2001-04-02