



Next: Interpretazione oggettivista e soggettivista
Up: Valutazioni e interpretazioni della
Previous: Probabilità e frequenza
Indice
Tabella:
Risultati della simulazione al computer di estrazioni
con probabilità a priori di successo pari a 1/2. 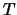 e
e 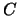 stanno
per ``testa'' e ``croce'' per analogia con il lancio di monete perfette.
stanno
per ``testa'' e ``croce'' per analogia con il lancio di monete perfette.
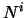 ,
, 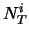 e
e 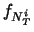 indicano il numero
di ``lanci'', il numero di ``teste'' e la loro frequenza relativa.
È
anche riportato il valore assoluto della differenza fra numero di
teste e ``numero'' di ``croci''.
indicano il numero
di ``lanci'', il numero di ``teste'' e la loro frequenza relativa.
È
anche riportato il valore assoluto della differenza fra numero di
teste e ``numero'' di ``croci''.
| i |
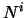 |
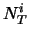 |
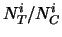 |
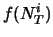 |
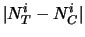 |
|
| 1 |
10 |
3 |
0.42857 |
0.3 |
4 |
|
| 2 |
100 |
53 |
1.12766 |
0.53 |
6 |
|
| 3 |
1000 |
484 |
0.93798 |
0.484 |
24 |
|
| 4 |
10000 |
4956 |
0.98255 |
0.4956 |
88 |
|
| 5 |
100000 |
49983 |
0.99932 |
0.49983 |
34 |
|
| 6 |
1000000 |
500475 |
1.00190 |
0.500475 |
950 |
|
| 7 |
10000000 |
5000790 |
1.00032 |
0.5000790 |
1580 |
|
|
Nel passato ha avuto grande importanza la
constatazione empirica che, per
i semplici casi in cui si sa calcolare la
probabilità mediante ragionamenti di simmetria (``definizione''
di Laplace), si nota che la frequenza relativa
``è in genere prossima''
al valore di probabilità calcolato a priori. In effetti,
sperimentalmente risulta che questo è ``praticamente vero''
quando il numero di prove è molto grande. In altri termini, maggiore
è il numero di prove e ``meno frequentemente succede''
di osservare grandi
scarti della frequenza dal valore di probabilità, ovvero
``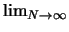 '' ''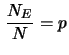 |
(2.4) |
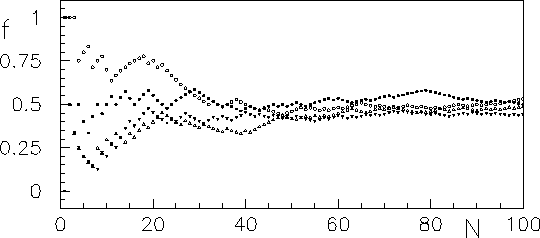
Figura:
Frequenza relativa dell'evento ``Testa''
in funzione del numero
di eventi in un esperimento
simulato del lancio di una moneta. Sono riportate quattro sequenze
indipendenti.
 |
Esempi (simulati al computer) di frequenza relativa in funzione
del numero dei lanci
di una moneta sono mostrati
nella tabella 2.1
e nella figura 2.1.
Questo tipo di osservazioni sperimentali ha condotto
ad enunciare la così detta
legge empirica del caso:
In una serie di prove ripetute un gran numero di volte nelle stesse
condizioni, ciascuno degli eventi possibili si manifesta con una
frequenza relativa che è circa uguale alla sua probabilità.
L'approssimazione migliora con il numero delle prove.
Questo fatto prettamente empirico ha suggerito di
ribaltare la (2.4) e
``definire''
la probabilità
in termini di frequenza relativa misurata in una successione
arbitrariamente grande di prove:
(il simbolo di limite è fra virgolette perché non ha niente a
che vedere con i limiti intesi in senso matematico).
L'interesse del collegamento fornito dalla legge empirica
del caso2.5consiste nel fatto di poter calcolare
la probabilità anche in quelle circostanze
in cui è difficile fare l'inventario
di tutti i casi possibili ed equiprobabili su cui si
basa la definizione classica di Laplace,
con la convinzione che si stia sostanzialmente determinando la
``stessa''
quantità.
Come fatto notare a proposito della
(2.4),
anche la (2.5) non va intesa come un limite nel senso
matematico. Non c'è infatti nessuna garanzia che
data una grandezza piccola 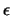 esista un
esista un 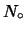 arbitrariamente grande tale che se
arbitrariamente grande tale che se 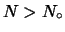 ci sia l'assoluta certezza
che la frequenza relativa differisca da
ci sia l'assoluta certezza
che la frequenza relativa differisca da  meno di
meno di 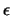 .
.




Next: Interpretazione oggettivista e soggettivista
Up: Valutazioni e interpretazioni della
Previous: Probabilità e frequenza
Indice
Giulio D'Agostini
2001-04-02

![]() esista un
esista un ![]() arbitrariamente grande tale che se
arbitrariamente grande tale che se ![]() ci sia l'assoluta certezza
che la frequenza relativa differisca da
ci sia l'assoluta certezza
che la frequenza relativa differisca da ![]() meno di
meno di ![]() .
.