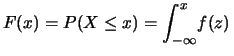Next: Funzione densità di probabilità
Up: Variabili casuali continue e
Previous: Probabilità nulle con diversi
Indice
È invece finita la
probabilità
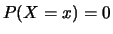 che la variabile sia compresa in un
certo intervallo.
Se la distanza fra i punti
che la variabile sia compresa in un
certo intervallo.
Se la distanza fra i punti  e
e 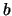 diventa infinitesima
anche la probabilità
sarà infinitesima.
diventa infinitesima
anche la probabilità
sarà infinitesima.
Se tutti i valori di  hanno lo stesso grado
di fiducia (e - si noti bene! -
non soltanto la stessa probabilità,
hanno lo stesso grado
di fiducia (e - si noti bene! -
non soltanto la stessa probabilità, 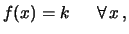 ), ovvero
), ovvero
la probabilità è proporzionale
all'ampiezza dell'intervallo e non dipende dal valore particolare
di  :
Quando l'intervallo diventa infinitesimo
:
Quando l'intervallo diventa infinitesimo
d
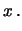
d
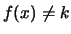
Nel caso generale (
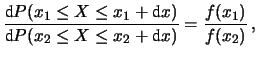 ) e considerando
due punti in corrispondenza dei quali
) e considerando
due punti in corrispondenza dei quali 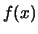 è continua
(almeno da una parte)
si ha che
il rapporto
fra le probabilità infinitesime intorno a tali punti è
proporzionale ai loro gradi di fiducia:
è continua
(almeno da una parte)
si ha che
il rapporto
fra le probabilità infinitesime intorno a tali punti è
proporzionale ai loro gradi di fiducia:
ovvero
d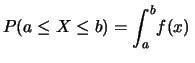 d d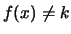 |
(8.1) |
Essendo i diversi valori di  a due a due
incompatibili, la probabilità su un intervallo finito
è data dalla somma degli infiniti
elementi di probabilità infinitesimi definiti dalla
(8.1)
a due a due
incompatibili, la probabilità su un intervallo finito
è data dalla somma degli infiniti
elementi di probabilità infinitesimi definiti dalla
(8.1)
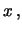 d d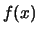 |
(8.2) |
avendo incluso il fattore di proporzionalità
della (8.1) nella definizione di 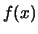 ,
ovvero l'elemento infinitesimo di probabilità
è definito essere esattamente
,
ovvero l'elemento infinitesimo di probabilità
è definito essere esattamente
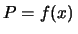 d
d :
:
d
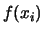
d
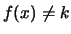




Next: Funzione densità di probabilità
Up: Variabili casuali continue e
Previous: Probabilità nulle con diversi
Indice
Giulio D'Agostini
2001-04-02
![]() hanno lo stesso grado
di fiducia (e - si noti bene! -
non soltanto la stessa probabilità,
hanno lo stesso grado
di fiducia (e - si noti bene! -
non soltanto la stessa probabilità, ![]() ), ovvero
), ovvero
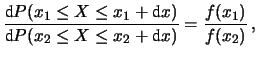 ) e considerando
due punti in corrispondenza dei quali
) e considerando
due punti in corrispondenza dei quali ![]() è continua
(almeno da una parte)
si ha che
il rapporto
fra le probabilità infinitesime intorno a tali punti è
proporzionale ai loro gradi di fiducia:
è continua
(almeno da una parte)
si ha che
il rapporto
fra le probabilità infinitesime intorno a tali punti è
proporzionale ai loro gradi di fiducia:
![]() a due a due
incompatibili, la probabilità su un intervallo finito
è data dalla somma degli infiniti
elementi di probabilità infinitesimi definiti dalla
(8.1)
a due a due
incompatibili, la probabilità su un intervallo finito
è data dalla somma degli infiniti
elementi di probabilità infinitesimi definiti dalla
(8.1)