



Next: Proprietà della funzione densità
Up: Variabili casuali continue e
Previous: Dal grado di fiducia
Indice
È immediato calcolare
la probabilità cumulativa, descritta dalla
funzione di ripartizione (chiamata talvolta semplicemente
integrale della funzione di probabilità o funzione
integrale):
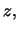 d d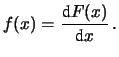 |
(8.3) |
(analogamente al caso delle
funzioni di distribuzione discrete, 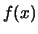 vale
0 al di fuori del campo di definizione della variabile casuale).
vale
0 al di fuori del campo di definizione della variabile casuale).
Dalla (8.3) segue che
Siccome 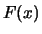 ha il significato di
probabilità,
ha il significato di
probabilità, 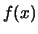 è una
``probabilità per unità di
è una
``probabilità per unità di  '', da cui il
nome di
funzione densità di probabilità, talvolta
indicata con p.d.f. (``probability
density function'').
Inoltre si vede come l'elemento infinitesimo
di probabilità, prima chiamato d
'', da cui il
nome di
funzione densità di probabilità, talvolta
indicata con p.d.f. (``probability
density function'').
Inoltre si vede come l'elemento infinitesimo
di probabilità, prima chiamato d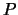 , può
essere anche indicato con
d
, può
essere anche indicato con
d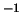 d
d .
.
Si noti anche come 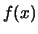 non sia una grandezza adimensionale.
Essendo
non sia una grandezza adimensionale.
Essendo 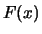 un numero puro, in quanto probabilità,
ne segue che
un numero puro, in quanto probabilità,
ne segue che 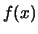 ha le dimensioni inverse di quelle di
ha le dimensioni inverse di quelle di  (ad esempio cm
(ad esempio cm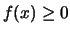 nell'esempio precedente
della caduta della pallina puntiforme).
nell'esempio precedente
della caduta della pallina puntiforme).




Next: Proprietà della funzione densità
Up: Variabili casuali continue e
Previous: Dal grado di fiducia
Indice
Giulio D'Agostini
2001-04-02
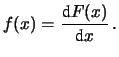
![]() non sia una grandezza adimensionale.
Essendo
non sia una grandezza adimensionale.
Essendo ![]() un numero puro, in quanto probabilità,
ne segue che
un numero puro, in quanto probabilità,
ne segue che ![]() ha le dimensioni inverse di quelle di
ha le dimensioni inverse di quelle di ![]() (ad esempio cm
(ad esempio cm![]() nell'esempio precedente
della caduta della pallina puntiforme).
nell'esempio precedente
della caduta della pallina puntiforme).