Next: Relazione fra esponenziale e
Up: Processo di Poisson -
Previous: Processo di Poisson -
Indice
Calcoliamo innanzitutto
la probabilità che non si verifichi nessun
``evento''8.5durante un certo tempo finito  . Lo facciamo in modo generale
considerando il numero aleatorio reale
. Lo facciamo in modo generale
considerando il numero aleatorio reale
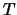 , definito come ``tempo di attesa
per registrare il primo conteggio, a partire da un certo istante arbitrario''.
Se, come fatto precedentemente, immaginiamo di suddividere il tempo
finito
, definito come ``tempo di attesa
per registrare il primo conteggio, a partire da un certo istante arbitrario''.
Se, come fatto precedentemente, immaginiamo di suddividere il tempo
finito  in
in  intervallini,
otteniamo (vedi distribuzione geometrica)
intervallini,
otteniamo (vedi distribuzione geometrica)
da cui segue la probabilità cumulativa
Quindi la funzione cumulativa dei tempi di attesa affinché
si verifichi un evento descritto
da un processo di Poisson è data da una esponenziale.
Per ottenere la funzione densità densità di probabilità
deriviamo la 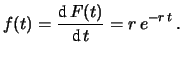 , ottenendo:
Introducendo la grandezza
, ottenendo:
Introducendo la grandezza 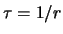 omogenea a
omogenea a  , otteniamo
l'espressione usuale della distribuzione esponenziale
nel dominio tempo (vedi (8.12).
, otteniamo
l'espressione usuale della distribuzione esponenziale
nel dominio tempo (vedi (8.12).
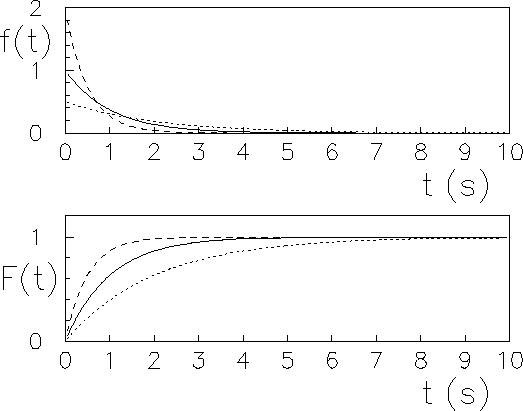
Figura:
Esempi di distribuzioni esponenziali nel dominio del tempo.
 |
Il parametro 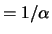 ha quindi il significato di previsione
del tempo di attesa prima che si verifichi il primo conteggio,
a partire da un istante arbitrario.
Essendo
ha quindi il significato di previsione
del tempo di attesa prima che si verifichi il primo conteggio,
a partire da un istante arbitrario.
Essendo 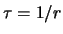 , tale previsione è pari all'inverso della
previsione del numero di eventi per unità di tempo.
, tale previsione è pari all'inverso della
previsione del numero di eventi per unità di tempo.
Si noti che essendo arbitrario
l'istante da cui parte l'osservazione,
esso può anche essere uno dei possibili conteggi.
Quindi la distribuzione trovata descrive il tempo di arrivo
fra due conteggi successivi.




Next: Relazione fra esponenziale e
Up: Processo di Poisson -
Previous: Processo di Poisson -
Indice
Giulio D'Agostini
2001-04-02
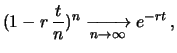
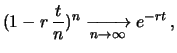
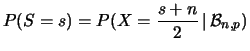
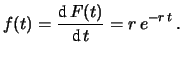 , ottenendo:
, ottenendo: