



Next: Tempo di attesa del
Up: Processo di Poisson -
Previous: Relazione fra esponenziale e
Indice
Relazione fra esponenziale e geometrica
Che l'esponenziale non sia altro che il limite
della geometrica per
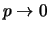 dovrebbe essere già chiaro
da come essa è stata introdotta. Facciamo altri chiarimenti:
dovrebbe essere già chiaro
da come essa è stata introdotta. Facciamo altri chiarimenti:
- quando
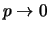 non ha più senso parlare
del numero di prova, in quanto le ``prove''
(ciascuna in un intervallino di tempo
non ha più senso parlare
del numero di prova, in quanto le ``prove''
(ciascuna in un intervallino di tempo
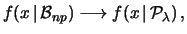 )
sono necessariamente infinite;
)
sono necessariamente infinite;
- così pure perde di significato
 per ``ciascuna'' prova (essa è pari a zero
indipendentemente dall'``intensità'' del processo)
e si può parlare
soltanto di
per ``ciascuna'' prova (essa è pari a zero
indipendentemente dall'``intensità'' del processo)
e si può parlare
soltanto di 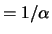 o di
o di  ;
;
- in particolare, ricordando le espressioni del valore atteso
le due distribuzioni, è possibile esprimere in modo analogo
 e
e  delle due distribuzioni:
delle due distribuzioni:
- geometrica:
 è pari al numero medio di successi
per estrazione;
è pari al numero medio di successi
per estrazione;
- esponenziale
 è pari al numero medio di successi per
unità di tempo (
è pari al numero medio di successi per
unità di tempo ( ha pertanto
il significato di ``intensità'' del processo di Bernoulli).
ha pertanto
il significato di ``intensità'' del processo di Bernoulli).
Un altro aspetto comune delle due distribuzioni
è la cosiddetta proprietà di assenza di memoria
delle due distribuzioni, espressa in generale come
(per l'esponenziale si sostituisca  a
a 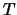 ),
facilmente dimostrabile dalla formula della probabilità
condizionata.
Vedremo una applicazione di tale proprietà nell'esempio dei
decadimenti radioattivi.
Si noti comunque come questa proprità di assenza di memoria
caratterizzi le due distribuzioni. Difatti è
possibile dimostrare come la richiesta
della (8.25) conduca alla geometrica
o all'esponenziale a seconda che si tratti di variabile discreta
o continua.
),
facilmente dimostrabile dalla formula della probabilità
condizionata.
Vedremo una applicazione di tale proprietà nell'esempio dei
decadimenti radioattivi.
Si noti comunque come questa proprità di assenza di memoria
caratterizzi le due distribuzioni. Difatti è
possibile dimostrare come la richiesta
della (8.25) conduca alla geometrica
o all'esponenziale a seconda che si tratti di variabile discreta
o continua.




Next: Tempo di attesa del
Up: Processo di Poisson -
Previous: Relazione fra esponenziale e
Indice
Giulio D'Agostini
2001-04-02
 è pari al numero medio di successi
per estrazione;
è pari al numero medio di successi
per estrazione;
 è pari al numero medio di successi per
unità di tempo (
è pari al numero medio di successi per
unità di tempo ( ha pertanto
il significato di ``intensità'' del processo di Bernoulli).
ha pertanto
il significato di ``intensità'' del processo di Bernoulli).