Concetto di probabilità condizionata

Se la valutazione di probabilità dipende dallo stato di informazione, non ha senso parlare di una ``probabilità assoluta''. Si può soltanto parlare di probabilità condizionata ad una certa informazione. Indichiamola genericamente con $P(E\,\vert\,I)$, letta ``probabilità di $E$ dato lo stato di informazione $I$'', o ``probabilità di $E$ data $I$''. Quando si parla di $P(E)$ senza aggiungere altro si fa riferimento a circostanze convenzionali, oppure - implicitamente - allo stato di informazione di chi la valuta.

Facciamo alcuni esempi:

• quando si dice che la probabilità della faccia di un dado sia 1/6 si sta assumendo che dado e lancio siano perfettamente regolari;
• quando si dice che la probabilità di Testa nel lancio di una moneta sia 1/2 si assume che la moneta sia regolare, che il lancio sia ``fatto a caso'' (non è irragionevole pensare ad un prestigiatore in grado di controllare il lancio) e che inoltre la moneta non cada verticale e non vada in un tombino (né che sia catturata al volo da un amico).

Quindi la probabilità va valutata entro lo spazio di possibilità di interesse. Ad esempio ci si può interessare alla probalità della faccia ``6'' del dado limitatamente al verificarsi di un numero pari ovvero $P(\lq\lq 6''\,\vert\,$``pari''$)=1/3$, oppure alla probabilità che la somma ottenuta in due lanci sia pari a 12 nelle stesse condizioni, cioè $P(\lq\lq$somma$= 12''\,\vert\,\lq\lq$entrambi$$   pari$'')=1/9$. Si noti che, più propriamente, bisognerebbe scrivere $P(\lq\lq 6''\,\vert\,$``pari'' & ``dado regolare''$)$ e $P(\lq\lq$somma$= 12''\,\vert\,$``entrambi pari'' & ``dado regolare''$)$, anche se nel seguito eviteremo di scrivere la condizione ``ovvia''^2.9.

Ragionamenti analoghi possono essere seguiti quando si voglia valutare la probabilità dalle frequenze (sempre nell'ipotesi che le clausole insite in tale valutazione siano soddisfatte). Si può quindi stimare la probabilità di furto di una macchina sotto la condizione che sia immatricolata a Milano, che il proprietario sia un venditore ambulante, che sia di una certa marca, o che le tre condizioni siano verificate simultaneamente (ammesso di trovare abbastanza macchine che corrispondano a tali requisiti per farne delle ``statistiche'').

Quindi nei due semplici casi di valutazione della probabilità dal giudizio di equiprobabilità e dalle frequenze relative del passato si ottiene:

$$P(E\,\vert\,C) = \frac{\mbox{numero di casi favorevoli a $E$\ e $C$}} {\mbox{numero di casi (equiprobabili) favorevoli a $C$}}$$ (2.6)

e

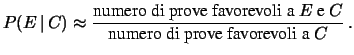$$P(E\,\vert\,C) \approx \frac{\mbox{numero di prove favorevoli a $E$\ e $C$}} {\mbox{numero di prove favorevoli a $C$}}\,.$$ (2.7)

Altre volte invece - nella maggior parte dei casi pratici della vita - lo stato di informazione cambia la valutazione, ma in modo più difficile da schematizzare: la probabilità di vittoria di un pilota di F1 dipende dal circuito e dalle condizioni ambientali (a parità di macchine); tutti sono d'accordo che la probabilità di vittoria di una squadra di calcio generalmente diminuisce se cinque titolari sono squalificati; la probabilità che un titolo azionario diminuisca di valore può dipendere dall'improvviso esonero dell'amministratore delegato (oppure può aumentare di quotazione se il dirigente allontanato era ritenuto incompetente).

Altri casi più prettamente scientifici nei quali non è possibile applicare le schematizzazioni di sopra sono quelli relativi alla probabilità di ipotesi scientifiche (teorie o valori di grandezze) alla luce di (``subordinate a'') osservazioni sperimentali. Ad esempio, quanto vali sono possibili valori di massa di un oggetto, se abbiamo letto $m_1$ su una bilancia? E come cambiano le mie credenze se pongo lo stesso oggetto su un'altra bilancia e leggo $x_2\ne x_1$? Anticipiamo che in molti casi di rilievo relativi alla ricerca e alla teoria dell'incertezza di misura la modifica della probabilità può essere effettata in modo logicamente consistente mediante un importante teorema del calcolo delle probabilità che vedremo a tempo debito.

Nel seguito, al fine di alleggerire la notazione, spesso scriveremo $P(E\vert I)$ semplicemente come $P(E)$, assumendo comunque che ci siano delle condizioni note a chi valuta la probabilità.