



Next: Proprietà formali di covarianza
Up: Covarianza e coefficiente di
Previous: Covarianza e coefficiente di
Indice
Facciamo un esempio numerico per capire meglio il problema.
Immaginiamo di dover lanciare 5 monete e di interessarci
alle variabili casuali 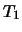 e
e 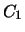 , numeri di teste e di croce.
Consideriamo anche un altro lancio di 5 monete
e chiamiamo
, numeri di teste e di croce.
Consideriamo anche un altro lancio di 5 monete
e chiamiamo 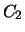 e
e 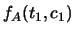 i rispettivi esiti.
Possiamo costruire le distribuzioni doppie
i rispettivi esiti.
Possiamo costruire le distribuzioni doppie
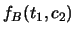 e
e
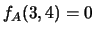 . Sebbene tutte le marginali
siano uguali e quindi tutte la variabili abbiano
un valore atteso 2.5 e una deviazione standard di 1.1, le due
distribuzioni sono completamente diverse (vedi tabella
9.2).
Ad esempio
. Sebbene tutte le marginali
siano uguali e quindi tutte la variabili abbiano
un valore atteso 2.5 e una deviazione standard di 1.1, le due
distribuzioni sono completamente diverse (vedi tabella
9.2).
Ad esempio
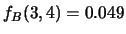 (evento impossibile),
mentre
(evento impossibile),
mentre
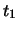 .
.
Tabella:
Distribuzioni congiunta del numero di teste e
numero di croci nel lancio di 5 monente (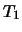 ,
, 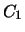 )
confrontata con quella del numero di teste e di croci relative
a due diversi lanci di monete. In valori sono in percentuale.
)
confrontata con quella del numero di teste e di croci relative
a due diversi lanci di monete. In valori sono in percentuale.
| |
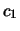 |
|
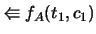 |
0 |
1 |
2 |
3 |
4 |
5 |
|
| 0 |
0 |
0 |
0 |
0 |
0 |
3.1 |
|
| 1 |
0 |
0 |
0 |
0 |
15.6 |
0 |
|
| 2 |
0 |
0 |
0 |
31.3 |
0 |
0 |
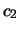 |
| 3 |
0 |
0 |
31.3 |
0 |
0 |
0 |
|
| 4 |
0 |
15.6 |
0 |
0 |
0 |
0 |
|
| 5 |
3.1 |
0 |
0 |
0 |
0 |
0 |
|
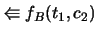 |
|
|
|
|
|
|
|
| 0 |
0.1 |
0.5 |
1.0 |
1.0 |
0.5 |
0.1 |
|
| 1 |
0.5 |
2.4 |
4.9 |
4.9 |
2.4 |
0.5 |
|
| 2 |
1.0 |
4.9 |
9.8 |
9.8 |
4.9 |
1.0 |
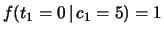 |
| 3 |
1.0 |
4.9 |
9.8 |
9.8 |
4.9 |
1.0 |
|
| 4 |
0.5 |
2.4 |
4.9 |
4.9 |
2.4 |
0.5 |
|
| 5 |
0.1 |
0.5 |
1.0 |
1.0 |
0.5 |
0.1 |
|
|
La differenza di rilievo fra le due distribuzioni
dell'esempio è che mentre nella prima ad ogni valore di
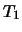 può essere associato un solo
valore di
può essere associato un solo
valore di 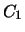 , nella seconda la conoscenza
di
, nella seconda la conoscenza
di 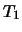 non modifica lo stato di incertezza rispetto a
non modifica lo stato di incertezza rispetto a
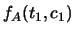 :
: 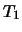 e
e 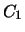 sono
dipendenti (o correlate);
sono
dipendenti (o correlate);
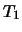 e
e 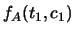 sono indipendenti (o scorrelate).
Questo fatto si riflette sulle distribuzioni condizionate,
le quali differiscono nei due casi. Ad esempio
sono indipendenti (o scorrelate).
Questo fatto si riflette sulle distribuzioni condizionate,
le quali differiscono nei due casi. Ad esempio
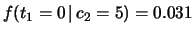 , mentre
, mentre
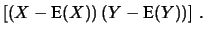 , e così via
, e così via
Dovendo quantificare il grado di correlazione con un solo
numero si utilizza il valore atteso del prodotto degli scarti
rispetto alle previsioni:
E
![$\displaystyle \left[\left(X-\mbox{E}(X)\right)
\left(Y-\mbox{E}(Y)\right)\right]\,.$](img2244.png)
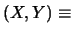 :
:
Cov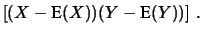 E E![$\displaystyle \left[(X-\mbox{E}(X)) (Y-\mbox{E}(Y))\right]\,.$](img2247.png) |
(9.16) |
Per capire come mai essa possa essere
adeguata9.3
allo scopo si pensi che
- se in corrispondenza di scarti positivi di
 (rispetto alla previsione)
si attendono (sempre in senso probabilistico)
scarti positivi anche per
(rispetto alla previsione)
si attendono (sempre in senso probabilistico)
scarti positivi anche per  , ne segue che
la previsione
del prodotto degli scarti è un numero positivo;
lo stesso è vero se,
in corrispondenza di scarti negativi di
, ne segue che
la previsione
del prodotto degli scarti è un numero positivo;
lo stesso è vero se,
in corrispondenza di scarti negativi di  ,
si attendono scarti negativi anche per
,
si attendono scarti negativi anche per  ;
;
- se invece si prevedono
scarti di segno opposto la covarianza è negativa;
- infine, la covarianza è nulla se si attendono
scarti mediamente incoerenti.
Ne segue che ci aspettiamo covarianza negativa fra 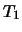 e
e 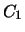 dell'esempio di tabella 9.2,
covarianza nulla fra
dell'esempio di tabella 9.2,
covarianza nulla fra
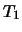 e
e 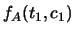 .
.
Per quanto riguarda il valore assoluto
della covarianza, esso non indica in maniera intuitiva
quanto due variabili sono correlate,
in quanto la covarianza non è
una grandezza omogenea con le due variabili casuali
e dipende anche dall'unità di misura scelta per le variabili.
Si preferisce rendere adimensionale la misura di
correlazione, dividendo per le scale naturali
degli scarti di ciascuna variabile, ovvero le due deviazioni standard.
Si definisce allora il coefficiente di correlazione, definito
come
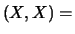 |
(9.17) |
Come detto a proposito della previsione e della sua incertezza,
in principio ci potrebbero essere modi alternativi
per riassumere con un numero
una caratteristica di una distribuzione. Volendo giustificare
questa scelta per la misura di correlazione, possiamo
fare le seguenti considerazioni:
- La covarianza è formalmente una estensione della
definizione operativa della varianza
a due variabili e quindi la covarianza di una variabile con sé
stessa è uguale alla varianza:
Cov
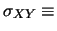
Var
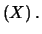
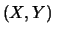 Cov Cov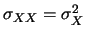 |
(9.18) |
con la convenzione che
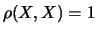 (questa notazione
sarà molto utile nelle applicazioni).
(questa notazione
sarà molto utile nelle applicazioni).
- Ne segue che il coefficiente di correlazione di una variabile con
sé stessa è uguale a 1 (
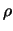 ): si dice che una variabile
è correlata al 100% con sé stessa.
): si dice che una variabile
è correlata al 100% con sé stessa.
- La covarianza, e quindi il coefficiente di correlazione, si annulla
se due variabili sono fra loro indipendenti, come abbiamo giustificato
intuitivamente sopra e come vedremo formalmente fra breve.
- Vedremo come la covarianza entra in modo naturale nel calcolo
della varianza di una combinazione lineare di variabili casuali
(paragrafo 9.5.2).
- Se due variabili sono legate (in modo deterministico)
da una relazione lineare,
il grado di correlazione misurato da
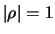 è massimo in modulo
(
è massimo in modulo
( )
e il suo segno dipende dal fatto che una variabile cresca o
diminuisca al crescere dell'altra, come intuitivamente comprensibile.
)
e il suo segno dipende dal fatto che una variabile cresca o
diminuisca al crescere dell'altra, come intuitivamente comprensibile.
La figura 9.2 mostra alcuni esempi di variabili doppie
discrete in cui la 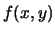 è proporzionali all'intensità
dei punti.
è proporzionali all'intensità
dei punti.
Figura:
Esempi di correlazione fra variabili casuali.
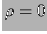 |
Si faccia attenzione come correlazioni complicate possano dare 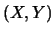 .
.




Next: Proprietà formali di covarianza
Up: Covarianza e coefficiente di
Previous: Covarianza e coefficiente di
Indice
Giulio D'Agostini
2001-04-02
![]() può essere associato un solo
valore di
può essere associato un solo
valore di ![]() , nella seconda la conoscenza
di
, nella seconda la conoscenza
di ![]() non modifica lo stato di incertezza rispetto a
non modifica lo stato di incertezza rispetto a
![]() :
: ![]() e
e ![]() sono
dipendenti (o correlate);
sono
dipendenti (o correlate);
![]() e
e ![]() sono indipendenti (o scorrelate).
Questo fatto si riflette sulle distribuzioni condizionate,
le quali differiscono nei due casi. Ad esempio
sono indipendenti (o scorrelate).
Questo fatto si riflette sulle distribuzioni condizionate,
le quali differiscono nei due casi. Ad esempio
![]() , mentre
, mentre
![]() , e così via
, e così via
 )
e il suo segno dipende dal fatto che una variabile cresca o
diminuisca al crescere dell'altra, come intuitivamente comprensibile.
)
e il suo segno dipende dal fatto che una variabile cresca o
diminuisca al crescere dell'altra, come intuitivamente comprensibile.