



Next: Somma di due variabili
Up: pzd100Soluzione generale per variabili
Previous: Trasformazione lineare di una
Indice
Se 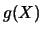 è una funzione che acquista
lo stesso valore di
è una funzione che acquista
lo stesso valore di 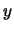 per più valori
di
per più valori
di  la procedura mostrata può essere utilizzata
in ciascuno dei tratti in cui la funzione è monotona.
Quindi si sommano i diversi termini che
contribuiscono allo stesso
la procedura mostrata può essere utilizzata
in ciascuno dei tratti in cui la funzione è monotona.
Quindi si sommano i diversi termini che
contribuiscono allo stesso 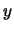 . Mostriamo il modo di operare
con un esempio particolare: il quadrato di
una variabile distribuita normalmente.
Per definizione abbiamo
. Mostriamo il modo di operare
con un esempio particolare: il quadrato di
una variabile distribuita normalmente.
Per definizione abbiamo
Confrontando questo risultato con la (8.43) si riconosce
nella  una variabile
di
una variabile
di 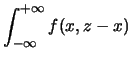 con un grado di libertà.
Questa identificazione deriva da un proprietà più generale, secondo cui
la somma dei quadrati di
con un grado di libertà.
Questa identificazione deriva da un proprietà più generale, secondo cui
la somma dei quadrati di  variabili normali standardizzate indipendenti
è descritta da una
variabili normali standardizzate indipendenti
è descritta da una 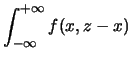 con
con 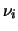 .
.




Next: Somma di due variabili
Up: pzd100Soluzione generale per variabili
Previous: Trasformazione lineare di una
Indice
Giulio D'Agostini
2001-04-02
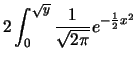
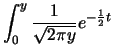 d
d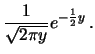 d
d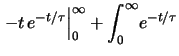
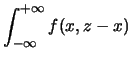 con un grado di libertà.
Questa identificazione deriva da un proprietà più generale, secondo cui
la somma dei quadrati di
con un grado di libertà.
Questa identificazione deriva da un proprietà più generale, secondo cui
la somma dei quadrati di 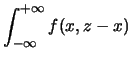 con
con