



Next: Fattori di influenza non
Up: Impostazione del problema. Caso
Previous: pzd100Derivazione di Gauss della
Indice
Anche se, per evitare ogni pedanteria, è stato suggerito
che, per i casi di routine, una prior uniforme è più
che ragionevole, un ricercatore esperto ha sempre delle
prior in mente, e con esse valuta il risultato.
Lo può accettare tranquillamente, diffidando quasi
sempre delle code di probabilità perché è ben cosciente dei
modelli matematici che usa; oppure si può insospettire
e controllare meglio lo strumento;
oppure può decidere di ripetere le misure, e così
via. Ad esempio, se si guarda al volo verso ora di pranzo
un orologio che non si sa essere
rotto e si legge 12:27 si prende per buona tale
osservazione (immagino che questa o analoghe
esperienze sia capitata a molti),
mentre se avesse indicato 17:43 la si sarebbe rifiutata.
Lo stesso vale per voltmetri rotti, termometro starati
e così via. Lo sperimentatore esperto ha sempre delle
prior che, pur nella loro vaghezza, sono molto solide
e filtrano le piccole disavventure che capitano in laboratorio.
Uno strumento rotto, un procedimento di misura sbagliato o
un errore di calcolo possono produrre effetti drammatici nel
risultato. Lo sperimentatore che ha buone prior, sviluppate
con anni di ricerca può sbagliare del 30%, del 50% o addirittura
di un fattore due, ma raramente di fattori 10, 100 o 1000.
Purtroppo questo discorso esula da questa trattazione e niente
può sostituire l'esperienza diretta. Vogliamo mostrare qui
soltanto un caso, molto schematizzato, di come comportarsi quando
il risultato ottenuto da una rapida applicazione delle
formule precedenti cozza violentemente con le proprie convinzioni.
Immaginiamo un esperimento progettato per misurare la massa
del neutrino (di tipo elettronico). Assumiamo che, la conoscenza
dettagliata dell'esperimento induca gli sperimentatori
a credere che le possibili osservazioni `equivalenti' (nel senso
specificato sopra, ovvero il numero al quale si arriva
avendo elaborato opportunamente la massa di dati) siano descritte
da una gaussiana centrata intorno alla massa vera, con deviazione
standard 3.3 eV/c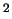 (per avere un'idea dell'ordine di grandezza,
in questa unità di misura la massa dell'elettrone è
511 mila, quella del protone 938 milioni). Alla fine
dell'esperimento si ottiene
(per avere un'idea dell'ordine di grandezza,
in questa unità di misura la massa dell'elettrone è
511 mila, quella del protone 938 milioni). Alla fine
dell'esperimento si ottiene  eV/c
eV/c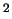 . Cosa dobbiamo
concluderne? Che il neutrino abbia, con probabilità
del 95% una massa negativa? Oppure che l'esperimento
sia ``sbagliato''? Se prima di questo esperimento i fisici
erano convinti che la massa del neutrino può essere al più
qualche decine di eV/c
. Cosa dobbiamo
concluderne? Che il neutrino abbia, con probabilità
del 95% una massa negativa? Oppure che l'esperimento
sia ``sbagliato''? Se prima di questo esperimento i fisici
erano convinti che la massa del neutrino può essere al più
qualche decine di eV/c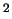 , come viene modificata la loro
conoscenza? (Si noti che sotto l'ipotesi ``esperimento sbagliato'' non
si impara niente).
, come viene modificata la loro
conoscenza? (Si noti che sotto l'ipotesi ``esperimento sbagliato'' non
si impara niente).
In questo caso, la prior forte è che la massa debba essere
non negativa. Inoltre si è praticamente convinti che essa
non può essere troppo grande (altrimenti avrebbe dato effetti
in altre osservazioni precedenti). Con queste considerazioni,
tenendo conto che l'esperimento è stato proposto, finanziato e
costruito con lo scopo di vedere qualcosa, si può modellizzare
l'incertezza in diversi modi (vedi figura 11.4):
Figura:
Esempio di inferenza in prossimità del limite
fisico di una grandezza (massa del neutrino in unità di eV/c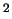 )
con tre diverse prior `motivate' e due diverse osservazioni. Si noti
come, nel caso dell'osservazione negativa (
)
con tre diverse prior `motivate' e due diverse osservazioni. Si noti
come, nel caso dell'osservazione negativa (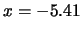 ) le tre distribuzioni
finali sono praticamente coincidenti.
) le tre distribuzioni
finali sono praticamente coincidenti.
 |
- Una distribuzione uniforme fra 0 e 30 eV/c
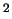 :
:
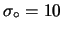 |
(11.22) |
- una mezza gaussiana centrata su zero con deviazione standard
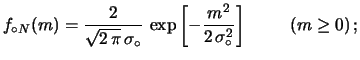 eV/c
eV/c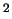 :
:
![$\displaystyle f_{\circ N}(m) =\frac{2}{\sqrt{2\,\pi}\,\sigma_\circ} \,\exp{\left[-\frac{m^2}{2\,\sigma_\circ^2}\right]} \hspace{1.0cm} (m \ge 0)\,;$](img3293.png) |
(11.23) |
- una distribuzione triangolare
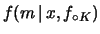 |
(11.24) |
La ``mezza-gaussiana'' ha il vantaggio di ammettere anche
valori di massa molto grandi, seppur molto poco plausibili.
Consideriamo per semplicità la distribuzione uniforme.
Inserendola nella formula di Bayes otteniamo
Come conclusione dell'esperimento, il valore al quale
crediamo di più è zero (moda),
ma 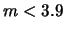 è diversa da zero fino a 30 eV/c
è diversa da zero fino a 30 eV/c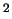 .
In questi casi è conveniente dare il risultato come limite
superiore ad un certo livello di probabilità.
Facendo i conti otteniamo:
.
In questi casi è conveniente dare il risultato come limite
superiore ad un certo livello di probabilità.
Facendo i conti otteniamo:
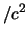 eV eV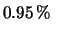 al al 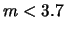 di probabilità di probabilità |
(11.27) |
Se avessimo usato le altre prior avremmo avuto
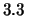 eV eV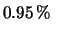 al al 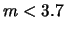 di probabilità di probabilità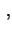 |
(11.28) |
praticamente lo stesso valore (soprattutto se confrontato
con la risoluzione sperimentale di
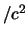 eV
eV ).
).
Ben diverso è il caso in cui si osserva un valore positivo ben distanziato
dallo zero, esemplificato in figura 11.4 dal punto
 . Sebbene l'inferenza dipende leggermente dalla prior (ma in modo
irrrilevante dal punto di vista pratico) si vede che anche la
banale inversione intuitiva di probabilità dà un risultato soddisfacente.
. Sebbene l'inferenza dipende leggermente dalla prior (ma in modo
irrrilevante dal punto di vista pratico) si vede che anche la
banale inversione intuitiva di probabilità dà un risultato soddisfacente.




Next: Fattori di influenza non
Up: Impostazione del problema. Caso
Previous: pzd100Derivazione di Gauss della
Indice
Giulio D'Agostini
2001-04-02
 eV/c
eV/c![]() (per avere un'idea dell'ordine di grandezza,
in questa unità di misura la massa dell'elettrone è
511 mila, quella del protone 938 milioni). Alla fine
dell'esperimento si ottiene
(per avere un'idea dell'ordine di grandezza,
in questa unità di misura la massa dell'elettrone è
511 mila, quella del protone 938 milioni). Alla fine
dell'esperimento si ottiene  eV/c
eV/c![]() . Cosa dobbiamo
concluderne? Che il neutrino abbia, con probabilità
del 95% una massa negativa? Oppure che l'esperimento
sia ``sbagliato''? Se prima di questo esperimento i fisici
erano convinti che la massa del neutrino può essere al più
qualche decine di eV/c
. Cosa dobbiamo
concluderne? Che il neutrino abbia, con probabilità
del 95% una massa negativa? Oppure che l'esperimento
sia ``sbagliato''? Se prima di questo esperimento i fisici
erano convinti che la massa del neutrino può essere al più
qualche decine di eV/c![]() , come viene modificata la loro
conoscenza? (Si noti che sotto l'ipotesi ``esperimento sbagliato'' non
si impara niente).
, come viene modificata la loro
conoscenza? (Si noti che sotto l'ipotesi ``esperimento sbagliato'' non
si impara niente).
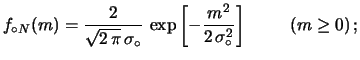 eV/c
eV/c![$\displaystyle f_{\circ N}(m) =\frac{2}{\sqrt{2\,\pi}\,\sigma_\circ} \,\exp{\left[-\frac{m^2}{2\,\sigma_\circ^2}\right]} \hspace{1.0cm} (m \ge 0)\,;$](img3293.png)
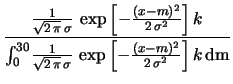
![$\displaystyle \frac{
\frac{1}{\sqrt{2\,\pi}\,\sigma}
\,\exp{\left[-\frac{(x-m)^...
...\pi}\,\sigma}
\,\exp{\left[-\frac{(x-m)^2}{2\,\sigma^2}\right]}
\,k\, \rm {d}m}$](img3296.png)
 . Sebbene l'inferenza dipende leggermente dalla prior (ma in modo
irrrilevante dal punto di vista pratico) si vede che anche la
banale inversione intuitiva di probabilità dà un risultato soddisfacente.
. Sebbene l'inferenza dipende leggermente dalla prior (ma in modo
irrrilevante dal punto di vista pratico) si vede che anche la
banale inversione intuitiva di probabilità dà un risultato soddisfacente.