



Next: pzd100Caso di forte vincolo
Up: Impostazione del problema. Caso
Previous: Effetto di una prior
Indice
pzd100Derivazione di Gauss
della gaussiana
A questo punto è interessante mostrare con quali argomenti
Gauss introdusse la funzione che porta il suo
nome11.4.
Essa era, infatti giaà nota molto primo di Gauss,
come limite della binomiale (vedi paragrafo 8.10).
L'interesse nella derivazione di Gauss è che essa
fu ottenuta nel contesto dell'inferenza probabilistica,
ma come soluzione di un problema inverso: qual'è la
forma più generale della verosimiglianza tale che il massimo
di probabilità di  coincida con la media aritmetica?
Nel risolvere questo problema,
dapprima Gausss derivò la formula della probabilità
delle ipotesi, assumendo equiprobabilità iniziale delle ipotesi.
In pratica ottenne il teorema di Bayes nel caso particolare
di probabilità iniziale delle ipotesi, concetto a lui
molto chiaro (``ante eventum cognitum'', contrapposto a
``post eventum cognitum'').
Quindi, passando alle osservazioni sperimentali
coincida con la media aritmetica?
Nel risolvere questo problema,
dapprima Gausss derivò la formula della probabilità
delle ipotesi, assumendo equiprobabilità iniziale delle ipotesi.
In pratica ottenne il teorema di Bayes nel caso particolare
di probabilità iniziale delle ipotesi, concetto a lui
molto chiaro (``ante eventum cognitum'', contrapposto a
``post eventum cognitum'').
Quindi, passando alle osservazioni sperimentali 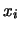 (usando
la nostra simbologia), cerca la forma della funzione incognita
(usando
la nostra simbologia), cerca la forma della funzione incognita
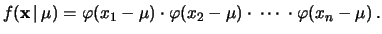 che descrive la probabilità di ottenere
che descrive la probabilità di ottenere 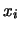 dal valore
vero
dal valore
vero  (sempre nella nostra simbologia). La
(funzione densità di) probabilità
del campione
(sempre nella nostra simbologia). La
(funzione densità di) probabilità
del campione
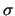 è allora data da
è allora data da
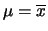 |
(11.18) |
A questo punto intervengono due ipotesi:
- Tutti i valori di
 sono ritenuti a priori
(``ante illa observationes'') ugualmente probabili
(``... aeque probabilia fuisse'').
sono ritenuti a priori
(``ante illa observationes'') ugualmente probabili
(``... aeque probabilia fuisse'').
- Il massimo di probabilità a posteriori
(``post illas observationes'')
si ottiene per
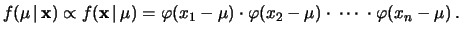 , media aritmetica degli
, media aritmetica degli  valori osservati.
valori osservati.
Dalla prima ipotesi segue
Per far uso della seconda, si impone che la derivata prima si annulli
in
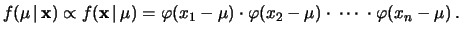 :
ovvero
ove
:
ovvero
ove
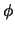 sta per la funzione derivata di
sta per la funzione derivata di 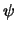 rispetto a
rispetto a  .
Chiamando
.
Chiamando 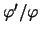 la funzione
la funzione
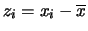 e indicando con
e indicando con
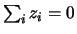 gli scarti dalla
media, i quali devono soddisfare la condizione
gli scarti dalla
media, i quali devono soddisfare la condizione
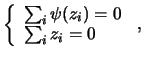 ,
abbiamo
,
abbiamo
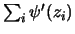 |
(11.19) |
la quale, dovendo essere valida indipendentemente da  e dal valore
degli scarti, dà il seguente
vincolo11.5 alla forma funzionale
di
e dal valore
degli scarti, dà il seguente
vincolo11.5 alla forma funzionale
di 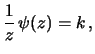 :
:
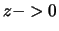 |
(11.20) |
con  costante (il limite
costante (il limite  non è un problema, in quanto
la derivata di
non è un problema, in quanto
la derivata di 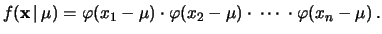 in
in 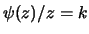 si annulla e la condizione
si annulla e la condizione
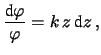 implica che numeratore e denominatore ci devono tendere
con la stessa ``rapidità).
Ne segue
Ovvero
implica che numeratore e denominatore ci devono tendere
con la stessa ``rapidità).
Ne segue
Ovvero
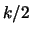 |
(11.21) |
ove 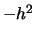 è stato chiamato
è stato chiamato 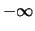 per imporre
che esso deve essere negativo in quanto
per imporre
che esso deve essere negativo in quanto 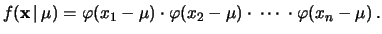 ha
il massimo in
ha
il massimo in 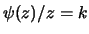 . Normalizzando la funzione mediante il suo integrale
da
. Normalizzando la funzione mediante il suo integrale
da 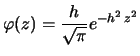 a
a 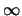 , conto dovuto a Laplace (``ab ill. Laplace
inventum''), la funzione ``di Gauss'' è (``funtio nostra fiet''):
.
, conto dovuto a Laplace (``ab ill. Laplace
inventum''), la funzione ``di Gauss'' è (``funtio nostra fiet''):
.




Next: pzd100Caso di forte vincolo
Up: Impostazione del problema. Caso
Previous: Effetto di una prior
Indice
Giulio D'Agostini
2001-04-02
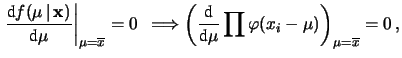
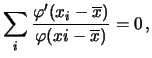
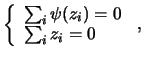 ,
abbiamo
,
abbiamo
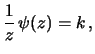 :
:
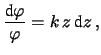 implica che numeratore e denominatore ci devono tendere
con la stessa ``rapidità).
Ne segue
implica che numeratore e denominatore ci devono tendere
con la stessa ``rapidità).
Ne segue
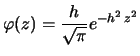 a
a