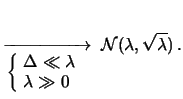Next: Proprietà riproduttiva della distribuzione
Up: Distribuzioni di probabilità di
Previous: Uso delle tabelle dell'integrale
Indice
pzd100Derivazione della
gaussiana come limite di
funzione binomiale o poissoniana
La figura 7.1 mostra come la distribuzione binomiale
ha una forma a campana che somiglia alla gaussiana, quando  ,
,
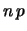 e
e 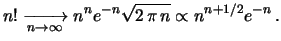 sono abbastanza grandi. È quindi interessante
trovare l'epressione asintotoca della binomiale. Questo problema
portò alla funzione che ora conosciamo come gaussiano quasi
un secolo prima della derivazione di Gauss, sulla quale ritorneremo
nel paragrafo 11.4.
Riscriviamo la funzione di probabilità binomiale riscrivendo
i fattoriali nella loro espressione asintotica data dalla formula di
Stirling (De Moivre e Stirling, più precisamente), che
ricordiamo qui:
Chiamando
sono abbastanza grandi. È quindi interessante
trovare l'epressione asintotoca della binomiale. Questo problema
portò alla funzione che ora conosciamo come gaussiano quasi
un secolo prima della derivazione di Gauss, sulla quale ritorneremo
nel paragrafo 11.4.
Riscriviamo la funzione di probabilità binomiale riscrivendo
i fattoriali nella loro espressione asintotica data dalla formula di
Stirling (De Moivre e Stirling, più precisamente), che
ricordiamo qui:
Chiamando
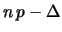 , da cui
, da cui
ne segue, omettendo di volta in volta
i fattori moltiplicativi che non dipendono
da 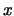 (ovvero da
(ovvero da 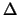 )
e che possiamo inglobare nella costante di normalizzazione:
)
e che possiamo inglobare nella costante di normalizzazione:
Per studiare il comportamento asintotico di 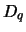 e
e 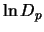 è preferibile passare ai logaritmi:
è preferibile passare ai logaritmi:
Per completezza, vediamo anche come si può arrivare
alla gaussiana come limite della poissoniana per
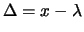 ,
ovvero quando i valori
,
ovvero quando i valori 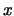 sui quali si addensa la massa di probabilità
sono relativamente prossimi a
sui quali si addensa la massa di probabilità
sono relativamente prossimi a 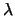 e lontani da zero.
Chiamando, in analogia al caso precedente
e lontani da zero.
Chiamando, in analogia al caso precedente
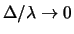 ,
prendiamo il logaritmo della funzione di distribuzione poissoniana e,
con l'ausilio dell'approssimazione di Stirling, facciamo il limite per
,
prendiamo il logaritmo della funzione di distribuzione poissoniana e,
con l'ausilio dell'approssimazione di Stirling, facciamo il limite per
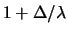 (ovvero siamo interessati a piccole
deviazioni dal valore atteso). Omettendo, come nel caso
precedente, i termini che di volta in volta
non dipendono da
(ovvero siamo interessati a piccole
deviazioni dal valore atteso). Omettendo, come nel caso
precedente, i termini che di volta in volta
non dipendono da 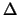 e sviluppando il logaritmo
di
e sviluppando il logaritmo
di
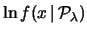 al secondo ordine intorno a 1, abbiamo:
al secondo ordine intorno a 1, abbiamo:
da cui segue
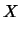 |
|
![$\displaystyle \xrightarrow[\left\{\!\begin{array}{l} \Delta\ll \lambda \\
\lambda\gg 0 \end{array}\right.
]{}\ {\cal N}(\lambda,\sqrt{\lambda})\,.$](img1963.png) |
(8.21) |




Next: Proprietà riproduttiva della distribuzione
Up: Distribuzioni di probabilità di
Previous: Uso delle tabelle dell'integrale
Indice
Giulio D'Agostini
2001-04-02
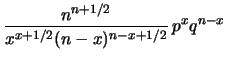
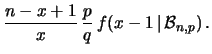
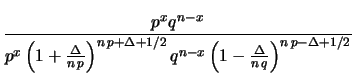
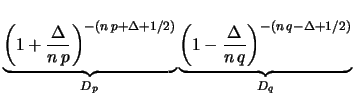
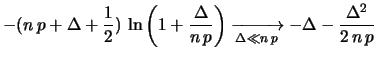
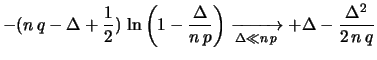
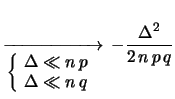
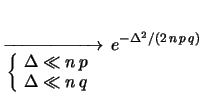
![$\displaystyle \xrightarrow[\left\{\!\begin{array}{l}\Delta\ll n\,p \\
\Delta\ll n\,q \end{array}\right.]{}
\,e^{-\Delta^2/(2\,n\,p\,q)}$](img1952.png)
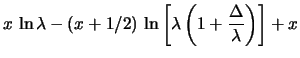
![$\displaystyle x\,\ln \lambda - (x+1/2)\,\ln \left[\lambda\left(
1+\frac{\Delta}{\lambda}\right)\right] + x$](img1960.png)
![$\displaystyle -\left(\lambda+\Delta+\frac{1}{2}\right)
\,\left[\frac{\Delta}{\lambda}-\frac{1}{2}\left(
\frac{\Delta}{\lambda}\right)^2\right] +\Delta$](img1961.png)