



Next: pzd100Derivazione della gaussiana come
Up: Distribuzioni di probabilità di
Previous: Distribuzione normale standardizzata
Indice
Esistono tabelle dell'integrale della ( 8.17)
espresso in genere come
8.4
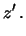 d d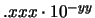 |
(8.19) |
Da queste tabelle è possibile calcolare qualsiasi altro integrale
facendo uso delle proprietà di simmetria della funzione e
dei valori notevoli di 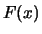 .
Un esempio è riportato in tabella 8.1.
.
Un esempio è riportato in tabella 8.1.
Tabella 8.1:
Tabella per il calcolo della funzione cumulativa
della distribuzione della normale.
|
|
|
|
|
|
|
|
|
|
|
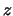 |
0.00 |
0.01 |
0.02 |
0.03 |
0.04 |
0.05 |
0.06 |
0.07 |
0.08 |
0.09 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.0 |
00000 |
00399 |
00798 |
01197 |
01595 |
01994 |
02392 |
02790 |
03188 |
03586 |
|
0.1 |
03983 |
04380 |
04776 |
05172 |
05567 |
05962 |
06356 |
06749 |
07142 |
07535 |
|
0.2 |
07926 |
08317 |
08706 |
09095 |
09483 |
09871 |
10257 |
10642 |
11026 |
11409 |
|
0.3 |
11791 |
12172 |
12552 |
12930 |
13307 |
13683 |
14058 |
14431 |
14803 |
15173 |
|
0.4 |
15542 |
15910 |
16276 |
16640 |
17003 |
17364 |
17724 |
18082 |
18439 |
18793 |
|
0.5 |
19146 |
19497 |
19847 |
20194 |
20540 |
20884 |
21226 |
21566 |
21904 |
22240 |
|
0.6 |
22575 |
22907 |
23237 |
23565 |
23891 |
24215 |
24537 |
24857 |
25175 |
25490 |
|
0.7 |
25804 |
26115 |
26424 |
26730 |
27035 |
27337 |
27637 |
27935 |
28230 |
28524 |
|
0.8 |
28814 |
29103 |
29389 |
29673 |
29955 |
30234 |
30511 |
30785 |
31057 |
31327 |
|
0.9 |
31594 |
31859 |
32121 |
32381 |
32639 |
32894 |
33147 |
33398 |
33646 |
33891 |
|
1.0 |
34134 |
34375 |
34614 |
34849 |
35083 |
35314 |
35543 |
35769 |
35993 |
36214 |
|
1.1 |
36433 |
36650 |
36864 |
37076 |
37286 |
37493 |
37698 |
37900 |
38100 |
38298 |
|
1.2 |
38493 |
38686 |
38877 |
39065 |
39251 |
39435 |
39617 |
39796 |
39973 |
40147 |
|
1.3 |
40320 |
40490 |
40658 |
40824 |
40988 |
41149 |
41309 |
41466 |
41621 |
41774 |
|
1.4 |
41924 |
42073 |
42220 |
42364 |
42507 |
42647 |
42785 |
42922 |
43056 |
43189 |
|
1.5 |
43319 |
43448 |
43574 |
43699 |
43822 |
43943 |
44062 |
44179 |
44295 |
44408 |
|
1.6 |
44520 |
44630 |
44738 |
44845 |
44950 |
45053 |
45154 |
45254 |
45352 |
45449 |
|
1.7 |
45543 |
45637 |
45728 |
45818 |
45907 |
45994 |
46080 |
46164 |
46246 |
46327 |
|
1.8 |
46407 |
46485 |
46562 |
46638 |
46712 |
46784 |
46856 |
46926 |
46995 |
47062 |
|
1.9 |
47128 |
47193 |
47257 |
47320 |
47381 |
47441 |
47500 |
47558 |
47615 |
47670 |
|
2.0 |
47725 |
47778 |
47831 |
47882 |
47932 |
47982 |
48030 |
48077 |
48124 |
48169 |
|
2.1 |
48214 |
48257 |
48300 |
48341 |
48382 |
48422 |
48461 |
48500 |
48537 |
48574 |
|
2.2 |
48610 |
48645 |
48679 |
48713 |
48745 |
48778 |
48809 |
48840 |
48870 |
48899 |
|
2.3 |
48928 |
48956 |
48983 |
49010 |
49036 |
49061 |
49086 |
49111 |
49134 |
49158 |
|
2.4 |
49180 |
49202 |
49224 |
49245 |
49266 |
49286 |
49305 |
49324 |
49343 |
49361 |
|
2.5 |
49379 |
49396 |
49413 |
49430 |
49446 |
49461 |
49477 |
49492 |
49506 |
49520 |
|
2.6 |
49534 |
49547 |
49560 |
49573 |
49585 |
49598 |
49609 |
49621 |
49632 |
49643 |
|
2.7 |
49653 |
49664 |
49674 |
49683 |
49693 |
49702 |
49711 |
49720 |
49728 |
49736 |
|
2.8 |
49744 |
49752 |
49760 |
49767 |
49774 |
49781 |
49788 |
49795 |
49801 |
49807 |
|
2.9 |
49813 |
49819 |
49825 |
49831 |
49836 |
49841 |
49846 |
49851 |
49856 |
49861 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.0 |
135-02 |
131-02 |
126-02 |
122-02 |
118-02 |
114-02 |
111-02 |
107-02 |
104-02 |
100-02 |
|
3.1 |
968-03 |
935-03 |
904-03 |
874-03 |
845-03 |
816-03 |
789-03 |
762-03 |
736-03 |
711-03 |
|
3.2 |
687-03 |
664-03 |
641-03 |
619-03 |
598-03 |
577-03 |
557-03 |
538-03 |
519-03 |
501-03 |
|
3.3 |
483-03 |
466-03 |
450-03 |
434-03 |
419-03 |
404-03 |
390-03 |
376-03 |
362-03 |
349-03 |
|
3.4 |
337-03 |
325-03 |
313-03 |
302-03 |
291-03 |
280-03 |
270-03 |
260-03 |
251-03 |
242-03 |
|
3.5 |
233-03 |
224-03 |
216-03 |
208-03 |
200-03 |
193-03 |
185-03 |
178-03 |
172-03 |
165-03 |
|
3.6 |
159-03 |
153-03 |
147-03 |
142-03 |
136-03 |
131-03 |
126-03 |
121-03 |
117-03 |
112-03 |
|
3.7 |
108-03 |
104-03 |
996-04 |
957-04 |
920-04 |
884-04 |
850-04 |
816-04 |
784-04 |
753-04 |
|
3.8 |
723-04 |
695-04 |
667-04 |
641-04 |
615-04 |
591-04 |
567-04 |
544-04 |
522-04 |
501-04 |
|
3.9 |
481-04 |
461-04 |
443-04 |
425-04 |
407-04 |
391-04 |
375-04 |
359-04 |
345-04 |
330-04 |
|
4.0 |
317-04 |
304-04 |
291-04 |
279-04 |
267-04 |
256-04 |
245-04 |
235-04 |
225-04 |
216-04 |
|
4.1 |
207-04 |
198-04 |
189-04 |
181-04 |
174-04 |
166-04 |
159-04 |
152-04 |
146-04 |
139-04 |
|
4.2 |
133-04 |
128-04 |
122-04 |
117-04 |
112-04 |
107-04 |
102-04 |
977-05 |
934-05 |
893-05 |
|
4.3 |
854-05 |
816-05 |
780-05 |
746-05 |
712-05 |
681-05 |
650-05 |
621-05 |
593-05 |
567-05 |
|
4.4 |
541-05 |
517-05 |
494-05 |
471-05 |
450-05 |
429-05 |
410-05 |
391-05 |
373-05 |
356-05 |
|
4.5 |
340-05 |
324-05 |
309-05 |
295-05 |
281-05 |
268-05 |
256-05 |
244-05 |
232-05 |
222-05 |
|
4.6 |
211-05 |
201-05 |
192-05 |
183-05 |
174-05 |
166-05 |
158-05 |
151-05 |
143-05 |
137-05 |
|
4.7 |
130-05 |
124-05 |
118-05 |
112-05 |
107-05 |
102-05 |
968-06 |
921-06 |
876-06 |
834-06 |
|
4.8 |
793-06 |
755-06 |
718-06 |
683-06 |
649-06 |
617-06 |
587-06 |
558-06 |
530-06 |
504-06 |
|
4.9 |
479-06 |
455-06 |
433-06 |
411-06 |
391-06 |
371-06 |
352-06 |
335-06 |
318-06 |
302-06 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Essa va letta nel seguente modo:
Figura:
Esempio
di calcolo dell'integrale della funzione normale standardizzata.
L'integrale della figura  è pari alla somma di quelli
di
è pari alla somma di quelli
di  e
e 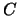 , leggibili dalle tabelle.
, leggibili dalle tabelle.
 |
La simmetria
della distribuzione normale permette di valutare dalle stesse tavole
anche l'integrale su un intervallo qualsiasi.
Figura:
Distribuzione normale standardizzata e intervalli di
probabilità.
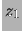 |
Facciamo alcuni esempi di integrali calcolati fra 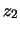 e
e 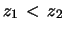 , con
, con
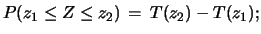 :
:
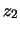 e
e 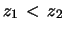 positivi:
positivi:
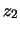 e
e 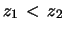 negativi:
negativi:
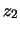 negativo e
negativo e 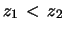 positivo:
positivo:
Alcuni esempi sono mostrati in figura 8.8.
Riportiamo la soluzione numerica ottenute mediante la tabella
8.1:
Terminiamo con un'ultima osservazione, implicita in quanto già detto:
la probabilità di trovare la variabile casuale
entro un certo numero di deviazioni standard non dipende
dai valori di  e di
e di  .
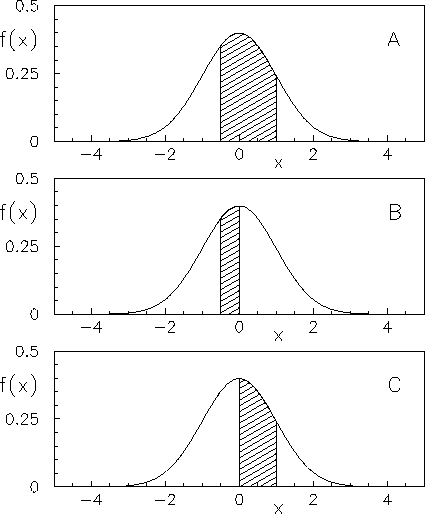
Diamo alcuni valori notevoli di probabilità (vedi anche figura
8.9):
.
Diamo alcuni valori notevoli di probabilità (vedi anche figura
8.9):
È interessante confrontare questo si ottiene entro 1 e 2  con quanto visto nel paragrafo 7.10.
con quanto visto nel paragrafo 7.10.
Per tornare ancora una volta sul fatto che la probabilità
che un numero aleatorio sia compreso nell'intervallo di 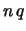 deviazione
standard dal valore atteso, mostriamo in figura
8.7 quattro diverse distribuzioni aventi tutte stesso
valore atteso e stessa deviazione standard.
deviazione
standard dal valore atteso, mostriamo in figura
8.7 quattro diverse distribuzioni aventi tutte stesso
valore atteso e stessa deviazione standard.




Next: pzd100Derivazione della gaussiana come
Up: Distribuzioni di probabilità di
Previous: Distribuzione normale standardizzata
Indice
Giulio D'Agostini
2001-04-02

![]() e di
e di ![]() .
Diamo alcuni valori notevoli di probabilità (vedi anche figura
8.9):
.
Diamo alcuni valori notevoli di probabilità (vedi anche figura
8.9):
![]() deviazione
standard dal valore atteso, mostriamo in figura
8.7 quattro diverse distribuzioni aventi tutte stesso
valore atteso e stessa deviazione standard.
deviazione
standard dal valore atteso, mostriamo in figura
8.7 quattro diverse distribuzioni aventi tutte stesso
valore atteso e stessa deviazione standard.