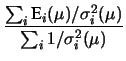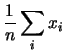Next: pzd100Derivazione di Gauss della
Up: Impostazione del problema. Caso
Previous: Verosimiglianza normale con nota
Indice
Effetto di una prior rilevante: combinazione
di risultati
A questo punto, una domanda naturale è cosa succede
se la prior non è proprio talmente vaga da essere ininfluente
sulla distribuzione di probabilità finale. Per semplificare
i conti, modellizziamo la nostra conoscenza a priori con una
gaussiana centrata in 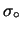 e di deviazione standard
e di deviazione standard
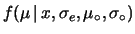 . Ad esempio, tale stato di conoscenza potrebbe
derivare da una precedente misura effettuata nelle condizioni
del paragrafo precedente. Come discusso a lungo nel capitolo
5, nello schema bayesiano il riaggiornamento
della probabilità si effettua usando come prior la distribuzione
finale dell'inferenza precedente. Nel nostro caso, abbiamo
. Ad esempio, tale stato di conoscenza potrebbe
derivare da una precedente misura effettuata nelle condizioni
del paragrafo precedente. Come discusso a lungo nel capitolo
5, nello schema bayesiano il riaggiornamento
della probabilità si effettua usando come prior la distribuzione
finale dell'inferenza precedente. Nel nostro caso, abbiamo
L'integrale è un po' più complicato del caso precedente.
Con le opportune semplificazoni11.3 il risultato dell'inferenza è:
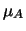 |
(11.7) |
con
I possibili
valori di  sono ancora descritti da una gaussiana
centrata in corrispondenza della
media pesata fra
sono ancora descritti da una gaussiana
centrata in corrispondenza della
media pesata fra  e
e 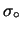 , con pesi
pari all'inverso delle varianze.
Previsione e
incertezza di previsione valgono
E
, con pesi
pari all'inverso delle varianze.
Previsione e
incertezza di previsione valgono
E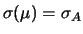 e
e
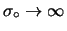 .
Il caso di prior vaga è recuperato per
.
Il caso di prior vaga è recuperato per
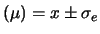 (con
(con 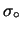 `ragionevole').
`ragionevole').
Poiché il risultato
E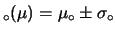 è quello che
si ottiene quando la prior è ininfluente, mentre la previsione
precedente
E
è quello che
si ottiene quando la prior è ininfluente, mentre la previsione
precedente
E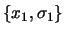 può essere pensato come dovuto ad una precedente inferenza,
le (11.8) e (eq:waver2) ci mostrano
come combinare due risultati
parziali. In particolare,
interpretando l'inverso
della varianza come peso statistico, la (11.9)
ci dice che il peso statistico risultante dall'inferenza
globale è pari alla somma dei pesi statistici delle inferenze
parziali.
può essere pensato come dovuto ad una precedente inferenza,
le (11.8) e (eq:waver2) ci mostrano
come combinare due risultati
parziali. In particolare,
interpretando l'inverso
della varianza come peso statistico, la (11.9)
ci dice che il peso statistico risultante dall'inferenza
globale è pari alla somma dei pesi statistici delle inferenze
parziali.
A questo punto, la combinazione di molti risultati
parziali indipendenti,
ciascuno ottenuto da una prior vaga è abbastanza
ovvio. È istruttivo ragionare in due modi diversi.
- Possiamo immaginare una catena di inferenze, del tipo
ove abbiamo indicato con
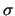 e
e
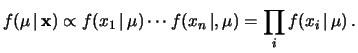 l'insieme dei valori osservati e delle deviazioni standard
legate alla verosimiglianza di ciascuna di esse. Applicando
iterativamente il teorema di Bayes abbiamo:
l'insieme dei valori osservati e delle deviazioni standard
legate alla verosimiglianza di ciascuna di esse. Applicando
iterativamente il teorema di Bayes abbiamo:
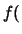 |
(11.10) |
- Il secondo modo consiste nel pensare alla verosimiglianza
congiunta di osservare
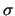 per ogni ipotesi di
per ogni ipotesi di
 :
:
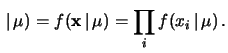 dati dati |
(11.11) |
Otteniamo lo stesso risultato indipendentemente dal percorso
seguito, il ché è confortante, visto che entrambi i
ragionamenti sono legittimi (vedi anche discussioni
in proposito nel capitolo
5).
In conclusione, abbiamo la seguente regola di combinazione:
che possiamo riscrivere,
facendo riferimento agli  valori osservati
valori osservati 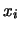 e
alle deviazioni standard delle relative verosimiglianze come
e
alle deviazioni standard delle relative verosimiglianze come
Si noti il carattere più generale delle (11.12)
e (11.13) rispetto a queste ultime, in quanto
quelle possono far riferimento a situazioni più complicate
delle semplici  osservazioni individuali. Ad esempio,
ciascuna previsone
E
osservazioni individuali. Ad esempio,
ciascuna previsone
E può derivare essa stessa
da una precedente combinazione o da un'analisi complicata.
può derivare essa stessa
da una precedente combinazione o da un'analisi complicata.
Figura:
Esempio di combinazione di quattro inferenze
indipendenti (curve tratteggiate) risultanti in un'unica
inferenza globale (curva tratteggiata).
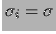 |
Un esempio di inferenza combinata è mostrata
in figura 11.3.
Tornando alle  osservazioni individuali indipendenti, vediamo il
caso in cui la deviazione standard sia la stessa per tutte
le osservazioni,
ovvero
osservazioni individuali indipendenti, vediamo il
caso in cui la deviazione standard sia la stessa per tutte
le osservazioni,
ovvero
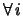
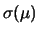 .
Le (11.14) e (
.
Le (11.14) e (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) diventano
) diventano
La previsione di  è pari alla media aritmetica
delle osservazioni. Inoltre, si vede come l'insieme delle
è pari alla media aritmetica
delle osservazioni. Inoltre, si vede come l'insieme delle
 osservazioni indipendenti hanno un peso statistico
di
osservazioni indipendenti hanno un peso statistico
di  volte quello di una singola osservazione.
volte quello di una singola osservazione.




Next: pzd100Derivazione di Gauss della
Up: Impostazione del problema. Caso
Previous: Verosimiglianza normale con nota
Indice
Giulio D'Agostini
2001-04-02
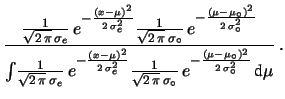
![]() è quello che
si ottiene quando la prior è ininfluente, mentre la previsione
precedente
E
è quello che
si ottiene quando la prior è ininfluente, mentre la previsione
precedente
E![]() può essere pensato come dovuto ad una precedente inferenza,
le (11.8) e (eq:waver2) ci mostrano
come combinare due risultati
parziali. In particolare,
interpretando l'inverso
della varianza come peso statistico, la (11.9)
ci dice che il peso statistico risultante dall'inferenza
globale è pari alla somma dei pesi statistici delle inferenze
parziali.
può essere pensato come dovuto ad una precedente inferenza,
le (11.8) e (eq:waver2) ci mostrano
come combinare due risultati
parziali. In particolare,
interpretando l'inverso
della varianza come peso statistico, la (11.9)
ci dice che il peso statistico risultante dall'inferenza
globale è pari alla somma dei pesi statistici delle inferenze
parziali.
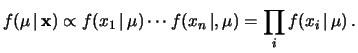 l'insieme dei valori osservati e delle deviazioni standard
legate alla verosimiglianza di ciascuna di esse. Applicando
iterativamente il teorema di Bayes abbiamo:
l'insieme dei valori osservati e delle deviazioni standard
legate alla verosimiglianza di ciascuna di esse. Applicando
iterativamente il teorema di Bayes abbiamo:
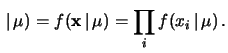 dati
dati può derivare essa stessa
da una precedente combinazione o da un'analisi complicata.
può derivare essa stessa
da una precedente combinazione o da un'analisi complicata.
![]() osservazioni individuali indipendenti, vediamo il
caso in cui la deviazione standard sia la stessa per tutte
le osservazioni,
ovvero
osservazioni individuali indipendenti, vediamo il
caso in cui la deviazione standard sia la stessa per tutte
le osservazioni,
ovvero
![]()
![]() .
Le (11.14) e (
.
Le (11.14) e (![]() ) diventano
) diventano