Verosimiglianza normale con
Innanzitutto, dal confronto fra i singoli valori
osservati e la loro media (o un valore vero convenzionale, nei
casi fortunati in cui si riesca a calibrare le misure su una
grandezza di riferimento) si nota che la distribuzione degli scarti
(``errori'') somiglia ad una gaussiana nel senso visto
a proposito dell'approssimazione normale di distribuzioni
di variabili casuali discrete (vedi paragrafo 10.10).
Come in quel
caso la gaussiana si estendeva per valori al di fuori del range
della variabile (tipicamente valori negativi, o valori maggiori di
![]() nel caso della binomiale), anche in questo caso bisogna
prestare attenzione a non prendere troppo
sul serio le code della gaussiana.
nel caso della binomiale), anche in questo caso bisogna
prestare attenzione a non prendere troppo
sul serio le code della gaussiana.
La seconda ragione è legata al teorema del limite centrale,
in base ad argomenti simili
a quelli per descrivere il
cammino casuale incontrato nel paragrafo
10.15.
Ammettiamo che nel processo di misura ci siano molti effetti
di disturbo, ovvero dei piccoli errori ![]() di valore atteso
nullo e deviazione standard
di valore atteso
nullo e deviazione standard 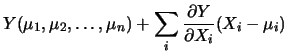 . L'errore totale
è dato da
. L'errore totale
è dato da
![]() , di varianza
, di varianza
![]() . Se valgono le condizioni
del teorema del limite centrale, ci aspettiamo che
. Se valgono le condizioni
del teorema del limite centrale, ci aspettiamo che ![]() sia descritto
da una gaussiana di valor medio zero e
deviazione standard
sia descritto
da una gaussiana di valor medio zero e
deviazione standard ![]() .
In genere questa approssimazione è abbastanza buona,
soprattutto perché
è frequente il caso in cui sono
le stesse
.
In genere questa approssimazione è abbastanza buona,
soprattutto perché
è frequente il caso in cui sono
le stesse ![]() ad essere descritte con buona approssimazione
da una gaussiana.
ad essere descritte con buona approssimazione
da una gaussiana.
Infine, a volte l'inferenza non è fatta a partire da una singola osservazione, ma dalla media di molte osservazioni, come se si trattasse di una singola osservazione equivalente. Questa operazione è legata al concetto statistico di sufficienza, su cui torneremo nel seguito (vedi paragrafo ***). Anche in questo caso, interviene il teorema del limite centrale che ci fa credere che questa `osservazione equivalente' può essere descritta da una gaussiana.
Stanti queste ipotesi (o ``credenze'' o
``assunzioni ragionevoli'' che dir si vogliano),
tendiamo a credere che la
singola osservazione (o osservazione equivalente) ![]() sarà descritta da
sarà descritta da
| (11.2) |
 :
:
Facciamo un esempio pratico. Il lettore vuole misurare la temperatura della stanza dove sta in quest'istante. Se vuole effettuare la misura, vuol dire che vuole conoscerla meglio di quanto ne sa in quest'istante, ma non che lui non ne sappia assolutamente niente. Qualsiasi persona è in genere in grado di indovinare la temperatura entro qualche grado, e per questo ci si stupisce quando un termometro indica valori molto diversi da quello che ci si aspetta (tanto da far sorgere il dubbio che il termometro sia rotto!). Quindi, nell'eseguire la misura si sceglierà lo strumento adatto, tale da migliorare la propria conoscenza. Se un amico ci desse uno strumento formidabile (per le sue potenzialità) in grado di misurare la temperatura assoluta da 0 a un milione di gradi entro un errore di 5 gradi, non lo accetteremmo per l'applicazione specifica: qualsiasi cosa leggeremo sullo strumento, crederemo ancora e soltanto a quanto possiamo indovinare dalla nostra sensazione fisiologica.
Riassumendo, nelle condizioni ordinarie delle misure, l'informazione
riassunta in
![]() è molto più vaga di quella
che ci può fornire lo strumento, ovvero
è molto più vaga di quella
che ci può fornire lo strumento, ovvero
![]() è molto più larga di
è molto più larga di
 , letta in funzione di
, letta in funzione di
![]() per
per ![]() fissato (dato).
Detto ancora in altri termini:
nella regione in cui la verosimiglianza varia rapidamente
(``su e giu'') intorno a
fissato (dato).
Detto ancora in altri termini:
nella regione in cui la verosimiglianza varia rapidamente
(``su e giu'') intorno a ![]() , la
, la
![]() è circa costante,
mentre per valori lontani da esso, le code gaussiane della
verosimiglianza rendono l'esatta forma di
è circa costante,
mentre per valori lontani da esso, le code gaussiane della
verosimiglianza rendono l'esatta forma di
![]() irrilevante.
Un esempio è mostrato in figura 11.2.
irrilevante.
Un esempio è mostrato in figura 11.2.
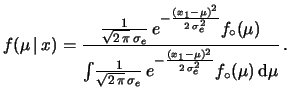
Quindi, quando valgono queste condizioni, si puù modellizzare la
conoscenza a priori come
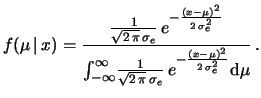 , costante in un intervallo
``abbastanza ampio''. Per sola convenienza matematica, estendiamo
tale intervallo a coprire l'intero asse reale. Ne segue che
nella (11.3) la
, costante in un intervallo
``abbastanza ampio''. Per sola convenienza matematica, estendiamo
tale intervallo a coprire l'intero asse reale. Ne segue che
nella (11.3) la
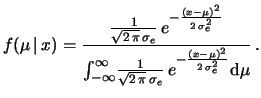 ,
si semplifica. Abbiamo allora:
,
si semplifica. Abbiamo allora:
| Livello di Probabilità | Intervallo di probabilità |
| (Livello di confidenza) | (Intervallo di confidenza) |
| 68.3% |
|
| 90.0% |
|
| 95.0% |
|
| 99.0% |
|
| 99.73% |
|