



Next: Verosimiglianza normale con nota
Up: Impostazione del problema. Caso
Previous: Impostazione del problema. Caso
Indice
Il problema dell'inferenza probabilistica è stato ampiamente
discusso nel capitolo ![[*]](file:/usr/lib/latex2html/icons/crossref.png) . In particolare,
partendo da esempi intuitivi,
è stata illustrata la potenza del teorema di Bayes
per riaggiornare la probabilità di ipotesi
alla luce di nuovi fatti. Successivamente, abbiamo visto,
rispettivamente nei paragrafi 7.16 e
9.3.3, come il teorema di Bayes si applicchi
sia a funzioni di probabilità che a funzioni di
densità di probabilità. Siccome in questa parte ci occuperemo
essenzialmente di grandezze il cui valore può assumere valori con
continuità, faremo uso della formula (9.12),
che riscriviamo qui nel seguente modo
. In particolare,
partendo da esempi intuitivi,
è stata illustrata la potenza del teorema di Bayes
per riaggiornare la probabilità di ipotesi
alla luce di nuovi fatti. Successivamente, abbiamo visto,
rispettivamente nei paragrafi 7.16 e
9.3.3, come il teorema di Bayes si applicchi
sia a funzioni di probabilità che a funzioni di
densità di probabilità. Siccome in questa parte ci occuperemo
essenzialmente di grandezze il cui valore può assumere valori con
continuità, faremo uso della formula (9.12),
che riscriviamo qui nel seguente modo
avendo indicato con  il valore vero
della grandezza che vogliamo inferire, con `dati'
i valori osservati e avendo omesso l'inessenziale
fattore di normalizzazione (come ampiamente discusso nel capitolo
il valore vero
della grandezza che vogliamo inferire, con `dati'
i valori osservati e avendo omesso l'inessenziale
fattore di normalizzazione (come ampiamente discusso nel capitolo
![[*]](file:/usr/lib/latex2html/icons/crossref.png) ). La condizione di sfondo
). La condizione di sfondo 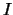 tiene conto
della globalità del nostro stato di informazione sulla misura
(grandezza da misurare, comportamento degli apparati e delle
procedure, condizioni ambientali, etc.).
Come discusso nell'introduzione
alle variabili casuali (paragrafo
tiene conto
della globalità del nostro stato di informazione sulla misura
(grandezza da misurare, comportamento degli apparati e delle
procedure, condizioni ambientali, etc.).
Come discusso nell'introduzione
alle variabili casuali (paragrafo ![[*]](file:/usr/lib/latex2html/icons/crossref.png) , in particolare
gli ultimi due punti), nell'impostazione seguita in questo testo
osservazioni e valori veri giocano un ruolo simmetrico.
, in particolare
gli ultimi due punti), nell'impostazione seguita in questo testo
osservazioni e valori veri giocano un ruolo simmetrico.
- Posso affermare quanto credo all'osservazione di certi dati sperimenatali,
subordinatamente ad ogni ipotesi di valore vero e delle
condizioni sperimentali, ossia esplicito
la mia verosimiglianza
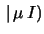 dati
dati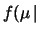 . E in questo
caso sono i valori dei dati ad essere numeri incerti.
. E in questo
caso sono i valori dei dati ad essere numeri incerti.
- Posso affermare quanto credo ai possibili valori di
 ,
subordinatamente all'osservazione di certi valori dei dati.
In questo caso è il valore vero
,
subordinatamente all'osservazione di certi valori dei dati.
In questo caso è il valore vero  ad essere un numero
incerto, mentre i dati sperimentali sono per definizione certi,
in quanto `dati'.11.1 Il risultato dell'esperimento
sarà quindi della forma
ad essere un numero
incerto, mentre i dati sperimentali sono per definizione certi,
in quanto `dati'.11.1 Il risultato dell'esperimento
sarà quindi della forma
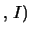 dati
dati , dove con
, dove con 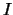 sono state indicate, ripetiamo,
tutte le informazioni di contorno su grandezza
da misurare, strumenti di misura e fattori di influenza.
sono state indicate, ripetiamo,
tutte le informazioni di contorno su grandezza
da misurare, strumenti di misura e fattori di influenza.
Lo schema generale di inferenza è illustrato in figura
11.1
Figura:
Schema generale del modello
modello inferenziale basato sulla probabilità condizionata.
L'asse delle  rappresenta il mondo reale delle osservazioni.
L'asse dei
rappresenta il mondo reale delle osservazioni.
L'asse dei  rappresenta invece i possibili valori dei parametri della
teoria, che, come tali, non si manifestano
direttamente ai nostri sensi.
rappresenta invece i possibili valori dei parametri della
teoria, che, come tali, non si manifestano
direttamente ai nostri sensi.
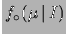 |
L'importanza concettuale
della prior
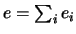 è stato discusso
nel capitolo
è stato discusso
nel capitolo ![[*]](file:/usr/lib/latex2html/icons/crossref.png) e verrà ripreso nel seguito,
mostrando come sia praticamente irrilevante nei casi di routine.
Si ricorda, infine, che il ruolo della verosimiglianza è quello
di modificare il grado di fiducia in ciascun valore di
e verrà ripreso nel seguito,
mostrando come sia praticamente irrilevante nei casi di routine.
Si ricorda, infine, che il ruolo della verosimiglianza è quello
di modificare il grado di fiducia in ciascun valore di  ,
come ovvio dalla formula (11.1).
,
come ovvio dalla formula (11.1).
Il resto del capitolo consisterà nell'applicazione sistematica
della formula (11.1) a diverse situazioni che si
verificano frequentemente nella pratica di laboratorio.
La condizione di contorno 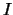 verrà in genere sottintesa,
a meno che non la si voglia esplicitare per tenere conto
dell'incertezza su grandezze di influenza (i cosiddetti
effetti sistematici).
verrà in genere sottintesa,
a meno che non la si voglia esplicitare per tenere conto
dell'incertezza su grandezze di influenza (i cosiddetti
effetti sistematici).
Vedremo anche come usare delle approssimazioni per semplicare i
conti nei semplici casi di routine.




Next: Verosimiglianza normale con nota
Up: Impostazione del problema. Caso
Previous: Impostazione del problema. Caso
Indice
Giulio D'Agostini
2001-04-02
 , dove con
, dove con ![]() verrà in genere sottintesa,
a meno che non la si voglia esplicitare per tenere conto
dell'incertezza su grandezze di influenza (i cosiddetti
effetti sistematici).
verrà in genere sottintesa,
a meno che non la si voglia esplicitare per tenere conto
dell'incertezza su grandezze di influenza (i cosiddetti
effetti sistematici).