



Next: Combinazione scettica
Up: Impostazione del problema. Caso
Previous: Conclusioni e raccomandazioni
Indice
Nei paragrafi precedenti abbiamo visto la funzione
 ,
interpretata come funzione di verosimiglianza di ottenere
un certo valore osservato data l'ipotesi
,
interpretata come funzione di verosimiglianza di ottenere
un certo valore osservato data l'ipotesi  . Interessiamoci
ora al problema di determinare veramente la probabilità
di un valore ignoto. Ci rendiamo conto che
. Interessiamoci
ora al problema di determinare veramente la probabilità
di un valore ignoto. Ci rendiamo conto che
 non è
sufficente. Infatti non siamo interessati alla probabilità
di
non è
sufficente. Infatti non siamo interessati alla probabilità
di  per ogni ipotesi
per ogni ipotesi  , bensì alla probabilità
che tenga conto di tutti i valori possibili di
, bensì alla probabilità
che tenga conto di tutti i valori possibili di  , pesati con la
loro plausibilità.
, pesati con la
loro plausibilità.
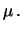 d d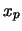 |
(11.102) |
Nel caso in cui la conoscenza di  ci deriva dall'aver osservato
il singolo (o valore equivalente) valore (passato)
ci deriva dall'aver osservato
il singolo (o valore equivalente) valore (passato) 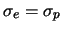 con
un esperimento avente deviazione standard
con
un esperimento avente deviazione standard
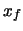 , e
il valore (futuro)
, e
il valore (futuro) 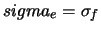 che andremo ad osservare deriverà
da un esperimento con
che andremo ad osservare deriverà
da un esperimento con
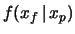 , abbiamo:
, abbiamo:
con
Si noti come la distribuzione predittiva (11.104)
descrive l'incertezza su un valore ignoto condizionata
da una precedente osservazione, essendo sparito il
``metafisico'' valore vero
(nel senso di non accessibile ai nostri sensi)  .
.
Figura:
Schema di inferenza predittiva attraverso
lo stadio intermedio ``metafisico''  .
.
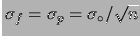 |
La figura 11.10 mostra lo schema di inferenza
dall'osservazione certa 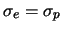 all'osservazione (futura) incerta
all'osservazione (futura) incerta
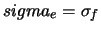 attraverso lo stadio intermedio non osservabile
attraverso lo stadio intermedio non osservabile  .
.
Si noti in particolare il caso di
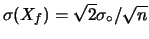 ,
ovvero di osservazioni equilavalenti ottenute nelle stesse condizioni
sperimentali e con la stessa quantità di osservazioni individuali.
Abbiamo
,
ovvero di osservazioni equilavalenti ottenute nelle stesse condizioni
sperimentali e con la stessa quantità di osservazioni individuali.
Abbiamo
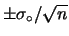 . In altri termini,
riteniamo probabile al 52% che la nuova media cada entro
. In altri termini,
riteniamo probabile al 52% che la nuova media cada entro
 da quella precedente.11.8
da quella precedente.11.8




Next: Combinazione scettica
Up: Impostazione del problema. Caso
Previous: Conclusioni e raccomandazioni
Indice
Giulio D'Agostini
2001-04-02
 ,
interpretata come funzione di verosimiglianza di ottenere
un certo valore osservato data l'ipotesi
,
interpretata come funzione di verosimiglianza di ottenere
un certo valore osservato data l'ipotesi  non è
sufficente. Infatti non siamo interessati alla probabilità
di
non è
sufficente. Infatti non siamo interessati alla probabilità
di 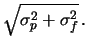

![]() ,
ovvero di osservazioni equilavalenti ottenute nelle stesse condizioni
sperimentali e con la stessa quantità di osservazioni individuali.
Abbiamo
,
ovvero di osservazioni equilavalenti ottenute nelle stesse condizioni
sperimentali e con la stessa quantità di osservazioni individuali.
Abbiamo
![]() . In altri termini,
riteniamo probabile al 52% che la nuova media cada entro
. In altri termini,
riteniamo probabile al 52% che la nuova media cada entro
 da quella precedente.11.8
da quella precedente.11.8