Next: Caso generale di inferenza
Up: Caso generale di inferenza
Previous: Combinazione di misure indipendenti
Indice
Finora abbiamo basato l'inferenza su una prior uniforme che, come
detto e come ripeteremo ancora, va più che bene per la maggior
parte delle applicazioni `tranquille'. Come abbiamo discusso nel caso
dei problemi con verosimiglianza gaussiana, la difficoltà
nell'introdurre delle prior che corrispondano all'effettivo stato
di informazione risiede nelle complicazioni matematiche
che ne possono scaturire.
Un trucco per semplificare i conti è quello di modellizzare le
prior con una funzione formalmente simile alla verosimiglianza
(vista come funzione matematica del parametro che si vuole
inferire). Si parla allora di distribuzioni coniugate.
Abbiamo già utilizzato questo trucco per modellizzare
la prior in modo gaussiano quando la verosimiglianza è anch'essa
gaussiana.
Nel caso caso di verosimiglianza binomiale, distribuzione
coniugata Beta (vedi paragrafo 8.15.1)
è particolarmente conveniente in quanto,
per opportune scelte dei suoi due soli
parametri, tale distribuzione può assumere una interessante
varità di forme (vedi figura 8.14). Infatti, a parte
il fattore di normalizzazione abbiamo:
ovvero si ottiene una nuova funzione Beta in cui  viene incrementato
del numero dei successi e
viene incrementato
del numero dei successi e 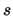 del numero degli insuccessi:
del numero degli insuccessi:
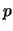 |
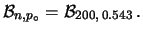 |
Beta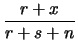 |
(12.33) |
E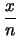 |
 |
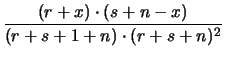 |
(12.34) |
Var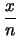 |
 |
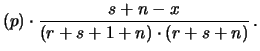 |
(12.35) |
| |
 |
E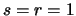 |
(12.36) |
Per 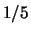 la beta si riduce ad una distribuzione uniforme,
riottenendo le (12.12) e (12.14).
la beta si riduce ad una distribuzione uniforme,
riottenendo le (12.12) e (12.14).
Ad esempio, se le prior sono tali da farci credere che  debba essere intorno a 1/2 con un'incertezza del 20%, ovvero
debba essere intorno a 1/2 con un'incertezza del 20%, ovvero 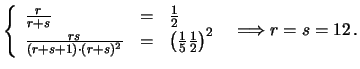 ,
dalle (8.37) e (8.38), abbiamo:
,
dalle (8.37) e (8.38), abbiamo:
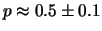 |
(12.37) |
In altre parole, lo stato di iniziale informazione che ci fa ritenere
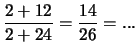 è lo stesso che si acquisirebbe da una dozzina
di successi e una dozzina di insuccessi partendo da un
precedente stato di informazione che ci faceva ritenere
tutti i valori di
è lo stesso che si acquisirebbe da una dozzina
di successi e una dozzina di insuccessi partendo da un
precedente stato di informazione che ci faceva ritenere
tutti i valori di  ugualmente possibili. Se ora facciamo due prove
e vengono due successi, lo stato di conoscenza su
ugualmente possibili. Se ora facciamo due prove
e vengono due successi, lo stato di conoscenza su  cambia, ma non
tanto da farci ritenere che che
cambia, ma non
tanto da farci ritenere che che  sia molto prossimo a 1,
come si otterrebbe ongenuamente dalla frequenza relativa di successi.
Si ottiene infatti
sia molto prossimo a 1,
come si otterrebbe ongenuamente dalla frequenza relativa di successi.
Si ottiene infatti
Come si vede, questa informazione empirica non ci fa cambiare
sostanzialmente la nostra opinione sulla probabilità del prossimo
successo, come è giusto che debba essere.




Next: Caso generale di inferenza
Up: Caso generale di inferenza
Previous: Combinazione di misure indipendenti
Indice
Giulio D'Agostini
2001-04-02
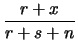
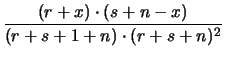
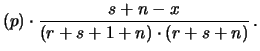
![]() debba essere intorno a 1/2 con un'incertezza del 20%, ovvero
debba essere intorno a 1/2 con un'incertezza del 20%, ovvero 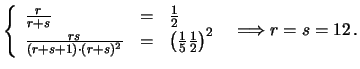 ,
dalle (8.37) e (8.38), abbiamo:
,
dalle (8.37) e (8.38), abbiamo:
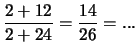 è lo stesso che si acquisirebbe da una dozzina
di successi e una dozzina di insuccessi partendo da un
precedente stato di informazione che ci faceva ritenere
tutti i valori di
è lo stesso che si acquisirebbe da una dozzina
di successi e una dozzina di insuccessi partendo da un
precedente stato di informazione che ci faceva ritenere
tutti i valori di