



Next: Caso di routine
Up: Verosimiglianza binomiale e poissoniana.
Previous: pzd100Uso della prior coniugata
Indice
 Caso generale di
inferenza con verosimiglianza poissoniana
Caso generale di
inferenza con verosimiglianza poissoniana
Sia ora 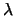 il parametro di interesse, avendo osservato
il parametro di interesse, avendo osservato
 conteggi in un intervallo di tempo
conteggi in un intervallo di tempo 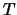 (o avendo osservato
contato
(o avendo osservato
contato  oggetti nel volume
oggetti nel volume 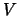 , e così via).
Il problema può essere anche impostato diversamente, inferendo
direttamente l'intensità del processo di Poisson
, e così via).
Il problema può essere anche impostato diversamente, inferendo
direttamente l'intensità del processo di Poisson  , ovvero
il tasso di conteggi, tale che
, ovvero
il tasso di conteggi, tale che
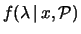 . Per ragioni didattiche
preferiamo provedere un passo alla volta.
. Per ragioni didattiche
preferiamo provedere un passo alla volta.
La verosimiglianza di osservare  per ogni ipotesi
per ogni ipotesi 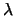 è data dalla distribuzione di Poisson. Applicando il teorema di Bayes,
abbiamo:
è data dalla distribuzione di Poisson. Applicando il teorema di Bayes,
abbiamo:
Per
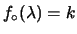 possiamo usare una distribuzione uniforme
fino ad un valore massimo molto più grande di
possiamo usare una distribuzione uniforme
fino ad un valore massimo molto più grande di  , che per
convenienza matematica possiamo estendere fino a infinito.
Quindi
, che per
convenienza matematica possiamo estendere fino a infinito.
Quindi
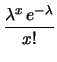 a numeratore e denominatore si semplificano
e, risolvendo per parti l'integrale di normalizzazione (come
per il caso gaussiano, siamo ``fortunati'' e l'integrale vale 1),
otteniamo
a numeratore e denominatore si semplificano
e, risolvendo per parti l'integrale di normalizzazione (come
per il caso gaussiano, siamo ``fortunati'' e l'integrale vale 1),
otteniamo
Come si vede, questa volta anche la funzione cumulativa
è relativamente semplice, ottenuta anch'essa mediante integrazione
per parti della funzione densità di probabilità.
Alcuni esempi sono mostrati in figura 12.2.
Figure 12.2 shows some numerical examples.
Figura:
Examples of
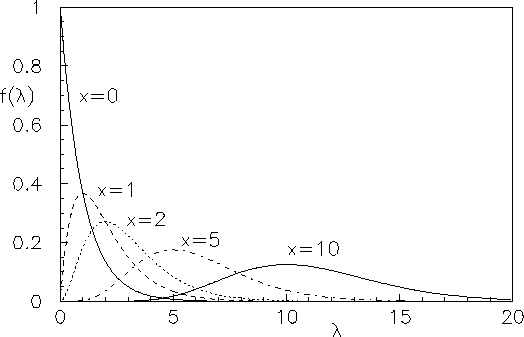 .
.
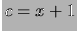 |
Si riconosce nella (12.41) una distribuzione Gamma
di parametri 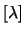 e
e  (vedi paragrafo ).
Ne segue che valore atteso, varianza e moda valgono
(vedi paragrafo ).
Ne segue che valore atteso, varianza e moda valgono
E![$\displaystyle [\lambda]$](img3630.png) |
 |
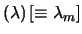 |
(12.43) |
Var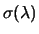 |
 |
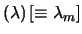 |
(12.44) |
Moda![$\displaystyle (\lambda)\,[\equiv\lambda_m]$](img3632.png) |
 |
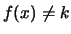 |
(12.45) |
Subsections




Next: Caso di routine
Up: Verosimiglianza binomiale e poissoniana.
Previous: pzd100Uso della prior coniugata
Indice
Giulio D'Agostini
2001-04-02
![]() per ogni ipotesi
per ogni ipotesi ![]() è data dalla distribuzione di Poisson. Applicando il teorema di Bayes,
abbiamo:
è data dalla distribuzione di Poisson. Applicando il teorema di Bayes,
abbiamo:
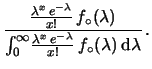
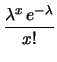 a numeratore e denominatore si semplificano
e, risolvendo per parti l'integrale di normalizzazione (come
per il caso gaussiano, siamo ``fortunati'' e l'integrale vale 1),
otteniamo
a numeratore e denominatore si semplificano
e, risolvendo per parti l'integrale di normalizzazione (come
per il caso gaussiano, siamo ``fortunati'' e l'integrale vale 1),
otteniamo