



Next: Inferenza sull'intensità del processo
Up: Caso generale di inferenza
Previous: Combinazione di risultati
Indice
Come si è già visto dai paragrafi precedenti, la verosimiglianza
vista come funzione matematica di 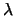 ha la struttura di una
distribuzione Gamma. Quindi questa è la
prior coniugata della poissoniana. Quindi, a parte i soliti
fattori moltiplicativi e considerando il caso generale
di
ha la struttura di una
distribuzione Gamma. Quindi questa è la
prior coniugata della poissoniana. Quindi, a parte i soliti
fattori moltiplicativi e considerando il caso generale
di  osservazioni, abbiamo:
osservazioni, abbiamo:
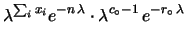 Gamma Gamma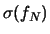 |
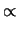 |
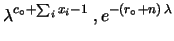 |
|
| |
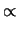 |
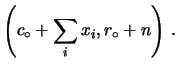 |
(12.59) |
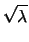 |
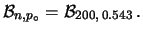 |
Gamma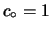 |
(12.60) |
Il caso di prior uniforme viene recuperato quando
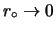 e
e
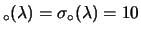 .
.
Come esempio, vediamo come modellizzare in modo più realistico
il caso in cui siano stati osservati 0 conteggi in un esperimento
in cui ``se attendevano pochi, non escludendo zero''. Questo
si verifica quando si cercano fenomeni rari. Un modo per
esprimere questa vaghezza in termini della Gamma può essere
di pensare ad un valore atteso di una decina con una incertezza
relativa del 100%, per fissare le idee, diciamo
E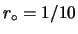 ,
ovvero
,
ovvero 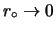 e
e
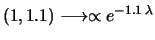 . Il risultato finale su
. Il risultato finale su 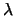 sarà
sarà
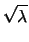 |
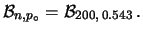 |
Gamma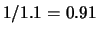 |
(12.61) |
E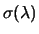 |
 |
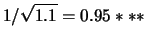 |
(12.62) |
E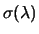 |
 |
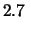 |
(12.63) |
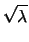 |
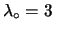 |
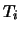 al 95% di probabilità al 95% di probabilità |
(12.64) |
Si noti che pur cambiando drasticamente la funzione a priori
(una prior uniforme ha valore atteso ``infinito'', nel senso che
è la metà del limite superiore, arbitrario) l'effetto sul risultato
finale è modesto (valore atteso, incertezza di previsione e
limite superiore al 95% cambiano di un 10%, che per questo tipo
di ricerca di frontiera è irrilevante, quelli che contano sono
gli ordini di grandezza).




Next: Inferenza sull'intensità del processo
Up: Caso generale di inferenza
Previous: Combinazione di risultati
Indice
Giulio D'Agostini
2001-04-02
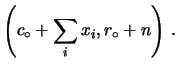
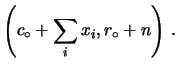
![]() ,
ovvero
,
ovvero ![]() e
e
![]() . Il risultato finale su
. Il risultato finale su ![]() sarà
sarà