



Next: Combinazione di risultati
Up: Caso generale di inferenza
Previous: Caso di routine
Indice
Anche in questo caso, vediamo il caso critico in cui
non è stato misurato alcun conteggio, pur non essendoci alcuna
ragione per cui si debba osservare esattamente zero e
``si sarebbero
potuti attendere anche numeri
diversi da zero con buona probabilità'' (questa espressione
sarà meglio formalizzata nel seguito, vedi paragrafo ***).
La figura 12.3 mostra
 . Il valore
al quale si crede di più è senz'altro 0, ma
la massa di probabilità si estende fino a diverse unità.
. Il valore
al quale si crede di più è senz'altro 0, ma
la massa di probabilità si estende fino a diverse unità.
Figura:
Upper limit to 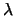 having observed 0 events.
having observed 0 events.
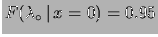 |
In questo caso è spesso di interesse dare un limite superiore
tale che la probabilità che 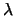 ecceda il limite sia ritenuta
piccola, per esempio il 10%, il 5% o l'1%. Scegliendo il 5% e
risolvendo l'equazione
ecceda il limite sia ritenuta
piccola, per esempio il 10%, il 5% o l'1%. Scegliendo il 5% e
risolvendo l'equazione
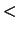 , otteniamo
, otteniamo
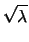 |
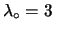 |
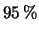 al al 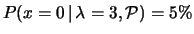 di probabilità di probabilità |
(12.52) |
Si noti come in questo caso vale anche
 , ma questa è una pura coincidenza
dovuta alle proprietà dell'esponenziale. Affermare che
``la probabilità che
, ma questa è una pura coincidenza
dovuta alle proprietà dell'esponenziale. Affermare che
``la probabilità che 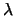 sia maggiore di 3, avendo osservato
zero, vale il 5% in quanto la probabilità che una poissoniana
di
sia maggiore di 3, avendo osservato
zero, vale il 5% in quanto la probabilità che una poissoniana
di 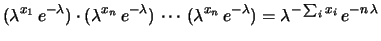 dia zero è del 5%'' è assolutamente scorretto.
Questa affermazione è ``innocua'' quando viene applicata al problema
in esame (il risultato è giusto per puro caso), ma è gravemente
fuorviante quando viene applicata ad altri problemi.
dia zero è del 5%'' è assolutamente scorretto.
Questa affermazione è ``innocua'' quando viene applicata al problema
in esame (il risultato è giusto per puro caso), ma è gravemente
fuorviante quando viene applicata ad altri problemi.




Next: Combinazione di risultati
Up: Caso generale di inferenza
Previous: Caso di routine
Indice
Giulio D'Agostini
2001-04-02
 . Il valore
al quale si crede di più è senz'altro 0, ma
la massa di probabilità si estende fino a diverse unità.
In questo caso è spesso di interesse dare un limite superiore
tale che la probabilità che
. Il valore
al quale si crede di più è senz'altro 0, ma
la massa di probabilità si estende fino a diverse unità.
In questo caso è spesso di interesse dare un limite superiore
tale che la probabilità che