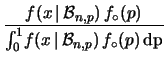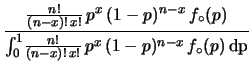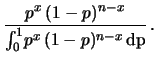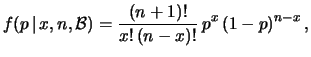Next: Caso di routine
Up: Verosimiglianza binomiale e poissoniana.
Previous: Caso binomiale
Indice
 Caso generale di inferenza con
verosimiglianza binomiale
Caso generale di inferenza con
verosimiglianza binomiale
Affrontiamo ora il caso generale dell'inferenza di  dalla conoscenza di
dalla conoscenza di  e di
e di  e dall'aver assunto un processo
di Bernoulli indipendente per ogni esito, sotto condizione
che
e dall'aver assunto un processo
di Bernoulli indipendente per ogni esito, sotto condizione
che  valga un certo valore (si potrebbe scrivere
``
valga un certo valore (si potrebbe scrivere
``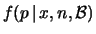 '', ma, come già
visto per
'', ma, come già
visto per  e
e  , per i parametri delle distribuzioni
preferiamo utilizzare soltanto la lettera minuscola).
Questo è stato il famoso ``problem in the theory of chance''
che aveva indotto il reverendo Bayes a sviluppare formalmente
il metodo di inversione di probabilità che porta il suo nome.
Assumendo una distribuzione
uniforme per
, per i parametri delle distribuzioni
preferiamo utilizzare soltanto la lettera minuscola).
Questo è stato il famoso ``problem in the theory of chance''
che aveva indotto il reverendo Bayes a sviluppare formalmente
il metodo di inversione di probabilità che porta il suo nome.
Assumendo una distribuzione
uniforme per  abbiamo:
abbiamo:
Questa volta l'integrale a denominatore è meno banale del caso
gaussiano. Il risultato finale è:
 |
(12.11) |
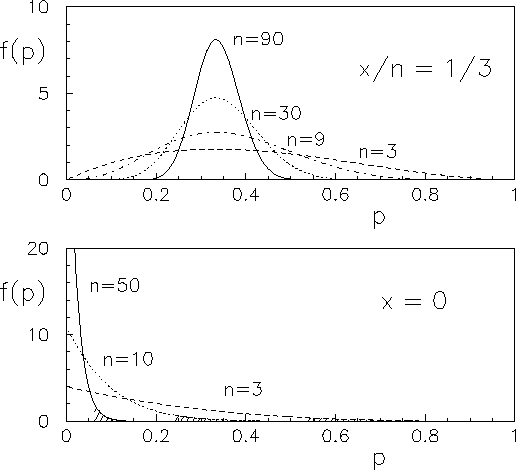
di cui sono mostrati alcuni esempi in Fig. 12.1.
Figura:
Funzione densità di probabilità del parametro  della binomiale, avendo osservato
della binomiale, avendo osservato  successi in
successi in  prove.
prove.
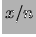 |
Si vede, come a parità di 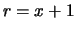 , al crescere di
, al crescere di  si è sempre
più sicuri su
si è sempre
più sicuri su  . Inoltre (semplice riflesso del
limite a normale della binomiale) per
. Inoltre (semplice riflesso del
limite a normale della binomiale) per  grande e
grande e 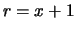 lontano da
0 e da 1 la funzione finale
lontano da
0 e da 1 la funzione finale 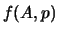 ha la forma gaussiana.
Valore atteso, varianza e moda di
ha la forma gaussiana.
Valore atteso, varianza e moda di 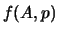 sono:12.1
sono:12.1
E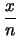 |
 |
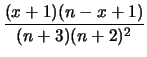 |
(12.12) |
Var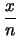 |
 |
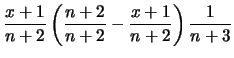 |
(12.13) |
| |
 |
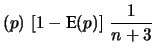 |
|
| |
 |
E![$\displaystyle (p)\,\left[1 - \mbox{E}(p)\right]\,\frac{1}{n+3}\,$](img3546.png) |
(12.14) |
Moda![$\displaystyle (p) \,\left[\equiv p_m \right]$](img3547.png) |
 |
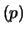 |
(12.15) |
Su questo problema aveva lavorato, oltre che Bayes,
anche Laplace e, in particolare,
la (12.12) è nota come formula recursiva di Laplace.
Si noti come essa sia dia valori di
E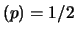 diversi da quelli
di sicurezza (ovvero 0 e 1) anche quando
diversi da quelli
di sicurezza (ovvero 0 e 1) anche quando  vale 0 o 1, consistente
con il fatto che una inferenza asata su processi aleatori non può mai
condurre alla sicurezza. Addirittura la formula dà una
risposta ragionevole (
E
vale 0 o 1, consistente
con il fatto che una inferenza asata su processi aleatori non può mai
condurre alla sicurezza. Addirittura la formula dà una
risposta ragionevole (
E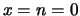 )
per
)
per 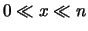 , ovvero prima di aver eseguito le misure. Questo non
ha niente di magico, ma è il solo riflesso della prior
uniforme su
, ovvero prima di aver eseguito le misure. Questo non
ha niente di magico, ma è il solo riflesso della prior
uniforme su  .
.
Subsections




Next: Caso di routine
Up: Verosimiglianza binomiale e poissoniana.
Previous: Caso binomiale
Indice
Giulio D'Agostini
2001-04-02