



Next: Coefficienti binomiali
Up: Disposizioni e combinazioni
Previous: Numero di permutazioni di
Indice
Combinazioni
In alcuni problemi non si ha interesse a distinguere fra
le 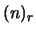 disposizioni semplici
tutte quelle che contengono gli stessi oggetti ma che differiscono
soltanto per l'ordine. Si parla allora
di ``combinazioni di
disposizioni semplici
tutte quelle che contengono gli stessi oggetti ma che differiscono
soltanto per l'ordine. Si parla allora
di ``combinazioni di  oggetti
oggetti  a
a  '',
indicato con
e letto ``n sopra r''. Esso si ottiene da
'',
indicato con
e letto ``n sopra r''. Esso si ottiene da 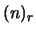 dividendolo per il
numero di ordinamenti diversi degli
dividendolo per il
numero di ordinamenti diversi degli  elementi:
elementi:
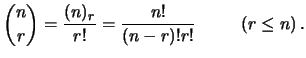 |
(3.6) |
Infatti, utilizzando la regola fondamentale del calcolo
combinatorio e chiamando provvisoriamente 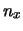 il numero
incognito che si vuole calcolare, abbiamo che il numero
di possibili scelte di
il numero
incognito che si vuole calcolare, abbiamo che il numero
di possibili scelte di  elementi fra
elementi fra  senza ripetizione
è pari al numero di combinazioni di
senza ripetizione
è pari al numero di combinazioni di  oggetti
oggetti  a
a  ,
moltiplicato per il numero di ordinamenti degli
,
moltiplicato per il numero di ordinamenti degli  elementi
di ciascuna combinazione:
elementi
di ciascuna combinazione:
da cui segue la (3.6).
La quantità `` sopra
sopra  ''
gode della proprietà di simmetria
''
gode della proprietà di simmetria
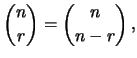 |
(3.7) |
ovvero è equivalente considerare gli  oggetti che si prendono
o gli
oggetti che si prendono
o gli 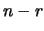 che si tralasciano.
Vale anche la relazione
che si tralasciano.
Vale anche la relazione
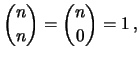 |
(3.8) |
la quale significa che c'è un solo modo di prendere o di tralasciare
tutti di  oggetti se non ci si interessa dell'ordine
(formalmente anche ``0 sopra 0'' vale 1, ma non
ha alcun significato applicativo).
oggetti se non ci si interessa dell'ordine
(formalmente anche ``0 sopra 0'' vale 1, ma non
ha alcun significato applicativo).
Esempi di combinazioni sono mostrati nelle figure
3.1 e 3.2.
Negli esempi del punto 4 otteniamo:
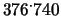 squadre e
378 (
squadre e
378 (
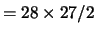 ) strette di mano.
) strette di mano.




Next: Coefficienti binomiali
Up: Disposizioni e combinazioni
Previous: Numero di permutazioni di
Indice
Giulio D'Agostini
2001-04-02
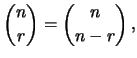
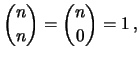
![]() squadre e
378 (
squadre e
378 (
![]() ) strette di mano.
) strette di mano.