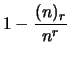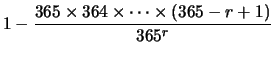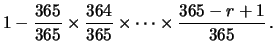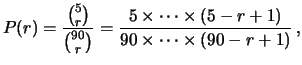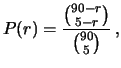- P. Massimo numero intero senza segno rappresentabile
con una parola di un computer
a 32 bit.
R. È equivalente al numero di parole di 32 lettere che si possono
formare da un alfabeto di 2 lettere (0, 1):
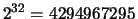 .
.
- P. Una moneta regolare viene lanciata
 volte. È più probabile
la sequenza con 50 teste o la sequenza con testa e croce alternate?
volte. È più probabile
la sequenza con 50 teste o la sequenza con testa e croce alternate?
R. Si tratta di r-disposizione di  oggetti (``T'', ``C'')
con
oggetti (``T'', ``C'')
con  . Il loro numero è
. Il loro numero è
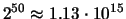 .
Assumendo l'indipendenza dei lanci
ogni sequenza ha la stessa probabilità
(
.
Assumendo l'indipendenza dei lanci
ogni sequenza ha la stessa probabilità
(
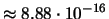 ).
).
- P.
Perché molti sono convinti che la sequenza che ha il
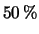 di teste
e il
di teste
e il 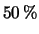 di croci sia più probabile di quella con tutte teste?
di croci sia più probabile di quella con tutte teste?
R. Si confonde la probabilità della singola sequenza con la
probabilità di una qualsiasi sequenza che abbia metà teste e metà
croci. Il numero totale di queste è dato da
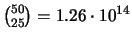 .
Queste sono in effetti l'11.2% del totale, ma purtroppo per vincere
bisogna indovinare quella giusta.
.
Queste sono in effetti l'11.2% del totale, ma purtroppo per vincere
bisogna indovinare quella giusta.
- P.
Calcolare la probabilità di estratto semplice,
ambo, terna,
quaderna e cinquina su una ruota del lotto (indipendentemente dall'ordine
di estrazione).
R. Il lotto ha  ``palline numerate''
(evitiamo di chiamarle ``numeri'' per evitare confusione)
delle quali ne vengono sorteggiate
``palline numerate''
(evitiamo di chiamarle ``numeri'' per evitare confusione)
delle quali ne vengono sorteggiate  .
Il numero di gruppi di
.
Il numero di gruppi di  elementi (con
elementi (con
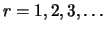 per
singolo estratto, ambo, terna, etc.) che si possono formare con le
per
singolo estratto, ambo, terna, etc.) che si possono formare con le 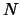 palline è:
palline è:
Di questi gruppi possibili,
quelli favorevoli per vincere sono quelli che
è possibile formare con le 5 palline estratte. Ne segue
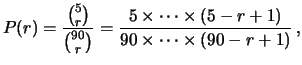 |
(3.14) |
da cui segue la formula ricorsiva
con
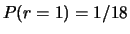 .
.
È interessante mostrare anche un altro modo di ragionare per ottenere
lo stesso risultato: ci sono
possibili cinquine.
Di queste ce ne sono
che contengono le  palline della scommessa (pari al numero
di combinazioni delle rimanenti
palline della scommessa (pari al numero
di combinazioni delle rimanenti
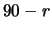 palline nelle
palline nelle 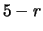 posizioni
che non interessano ai fini della scommessa).
Ne segue
posizioni
che non interessano ai fini della scommessa).
Ne segue
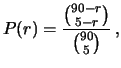 |
(3.15) |
che ovviamente dà gli stessi
risultati della (3.14).
- P.
Quanto vale la probabilità che in un gruppo di
 persone ce ne siano almeno due che hanno il compleanno lo stesso giorno?
(Si assuma una distribuzione uniforme nelle nascite nei 365 giorni
dell'anno e si trascurino per semplicità i bisestili.)
persone ce ne siano almeno due che hanno il compleanno lo stesso giorno?
(Si assuma una distribuzione uniforme nelle nascite nei 365 giorni
dell'anno e si trascurino per semplicità i bisestili.)
Tabella:
Probabilità che in un gruppo di  persone
almeno due abbiano il compleanno lo stesso giorno. Il calcolo
è basato sull'equiprobabilità delle nascite e trascurando
l'effetto degli anni bisestili
persone
almeno due abbiano il compleanno lo stesso giorno. Il calcolo
è basato sull'equiprobabilità delle nascite e trascurando
l'effetto degli anni bisestili
 |
5 |
10 |
15 |
20 |
23 |
30 |
41 |
46 |
57 |
70 |
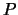 (%) (%) |
2.7 |
11.7 |
25.3 |
41.1 |
50.7 |
70.6 |
90.3 |
94.8 |
99.0 |
99.9
|
|
R. Conviene partire dalla probabilità che tutte le  persone
abbiano
compleanni diversi, ovvero che
persone
abbiano
compleanni diversi, ovvero che  giorni estratti fra
i 365 giorni dell'anno
siano tutti differenti.
Essa, data l'ipotesi di equiprobabilità, si riduce al calcolo del
numero dei casi possibili (pari alle
giorni estratti fra
i 365 giorni dell'anno
siano tutti differenti.
Essa, data l'ipotesi di equiprobabilità, si riduce al calcolo del
numero dei casi possibili (pari alle  -disposizioni
di
-disposizioni
di  oggetti) e a quello dei casi favorevoli (pari alle
oggetti) e a quello dei casi favorevoli (pari alle  -disposizioni
semplici di
-disposizioni
semplici di  oggetti):
oggetti):
In tabella 3.2 è riportata 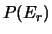 per alcuni valori
di
per alcuni valori
di  . Si tenga conto che in realtà le nascite non sono distribuite
uniformemente, ma si verificano più spesso in alcuni periodi
dell'anno. Questo effetto tende a far aumentare la probabilità di
coincidenze di compleanno (si immagini se, ad esempio,
il 90% delle nascite
si verificasse concentrate in un solo mese
e il restante 10% negli altri mesi dell'anno).
. Si tenga conto che in realtà le nascite non sono distribuite
uniformemente, ma si verificano più spesso in alcuni periodi
dell'anno. Questo effetto tende a far aumentare la probabilità di
coincidenze di compleanno (si immagini se, ad esempio,
il 90% delle nascite
si verificasse concentrate in un solo mese
e il restante 10% negli altri mesi dell'anno).
![]() .
.
![]() oggetti (``T'', ``C'')
con
oggetti (``T'', ``C'')
con ![]() . Il loro numero è
. Il loro numero è
![]() .
Assumendo l'indipendenza dei lanci
ogni sequenza ha la stessa probabilità
(
.
Assumendo l'indipendenza dei lanci
ogni sequenza ha la stessa probabilità
(
![]() ).
).
![]() .
Queste sono in effetti l'11.2% del totale, ma purtroppo per vincere
bisogna indovinare quella giusta.
.
Queste sono in effetti l'11.2% del totale, ma purtroppo per vincere
bisogna indovinare quella giusta.
![]() ``palline numerate''
(evitiamo di chiamarle ``numeri'' per evitare confusione)
delle quali ne vengono sorteggiate
``palline numerate''
(evitiamo di chiamarle ``numeri'' per evitare confusione)
delle quali ne vengono sorteggiate ![]() .
Il numero di gruppi di
.
Il numero di gruppi di ![]() elementi (con
elementi (con
![]() per
singolo estratto, ambo, terna, etc.) che si possono formare con le
per
singolo estratto, ambo, terna, etc.) che si possono formare con le ![]() palline è:
palline è:
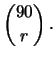
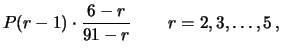
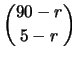
![]() persone
abbiano
compleanni diversi, ovvero che
persone
abbiano
compleanni diversi, ovvero che ![]() giorni estratti fra
i 365 giorni dell'anno
siano tutti differenti.
Essa, data l'ipotesi di equiprobabilità, si riduce al calcolo del
numero dei casi possibili (pari alle
giorni estratti fra
i 365 giorni dell'anno
siano tutti differenti.
Essa, data l'ipotesi di equiprobabilità, si riduce al calcolo del
numero dei casi possibili (pari alle ![]() -disposizioni
di
-disposizioni
di ![]() oggetti) e a quello dei casi favorevoli (pari alle
oggetti) e a quello dei casi favorevoli (pari alle ![]() -disposizioni
semplici di
-disposizioni
semplici di ![]() oggetti):
oggetti):