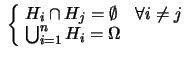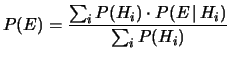Next: Indipendenza logica e indipendenza
Up: Altre proprietà della probabilità
Previous: Legge della moltiplicazione
Indice
Legge delle alternative
Ricordiamo la formula che esprime la probabilità di un certo
evento  come somma delle probabilità di tutti i prodotti
logici dell'evento
come somma delle probabilità di tutti i prodotti
logici dell'evento  con ciascuno degli eventi di una classe completa
(vedi 4.6):
con ciascuno degli eventi di una classe completa
(vedi 4.6):
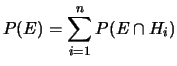 se se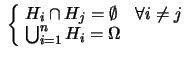 |
(4.25) |
Applicando a ciascuno dei prodotti logici il teorema delle probabilità
composte otteniamo
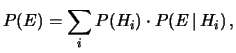 |
(4.26) |
conosciuta come legge delle alternativa o
formula di disintegrazione
(si incontra anche la denominazione formula delle probabilità
totali, ma non va confusa con l'omonima
(4.5)!).
Anche se la relazione è una semplice conseguenza della
(4.6) e del teorema delle probabilità composte,
essa è molto importante sia per le applicazioni che per una migliore
``visualizzazione'' della probabilità condizionata. Infatti:
Figura:
Legge delle alternative (o formula di
disintegrazione) nel punto di vista dei
percorsi alternativi che conducono ad un certo evento.
 |




Next: Indipendenza logica e indipendenza
Up: Altre proprietà della probabilità
Previous: Legge della moltiplicazione
Indice
Giulio D'Agostini
2001-04-02
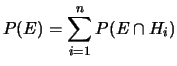 se
se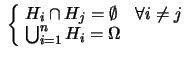
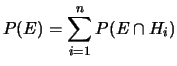 se
se