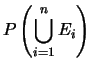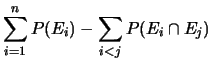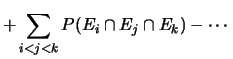Next: pzd100Dimostrazioni delle proprietà della
Up: Regole della probabilità
Previous: Evento condizionato
Indice
Abbiamo incontrato alcune regole a cui la valutazione
della probabilità deve
soddisfare, derivate dal concetto di scommessa coerente: la
probabilità deve essere compresa fra zero e 1;
vale 1 per l'evento certo e 0 per quello impossibile;
vale la regola di somma per probabilità di eventi incompatibili.
Da queste regole, mediante le proprietà formali degli eventi
e degli insiemi è possibile derivare altre proprietà cui la
probabilità deve soddisfare.
È possibile dimostrare facilmente che queste regole di base
sono soddisfatte automaticamente
anche dalle valutazioni combinatorie
e frequentiste.
Esiste un approccio molto formale alla probabilità in cui
le tre regole di base sono assunte come assiomi e
le proprietà che ne seguono sono ricavate come teoremi.
In questo approccio però
la probabilità non è definita come concetto,
così come anche l'evento è soltanto un oggetto matematico.
In questa teoria la probabilità è semplicemente un numero
reale che soddisfi i tre assiomi dati
dalle regole4.2:
- Regola 1
- (positività):
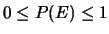 ;
;
- Regola 2
- (certezza):
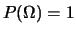 ,
,
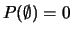 ;
;
- Regola 3
- (unione):
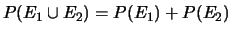 , se
, se
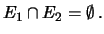
In particolare, la Regola 3 può essere estesa ad un
numero4.3  di eventi:
di eventi:
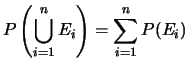 se se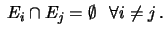 |
(4.5) |
Questa relazione è nota con il nome di teorema delle probabilità totali.
Da queste regole di base seguono alcune relazioni importanti
che devono essere sempre soddisfatte dalle
valutazioni della probabilità:
- Proprietà 1
- :
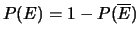 .
.
- Proprietà 2
- :
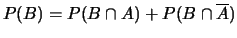 . Questa proprietà
può essere estesa ad una classe completa di eventi,
ottenendo
. Questa proprietà
può essere estesa ad una classe completa di eventi,
ottenendo
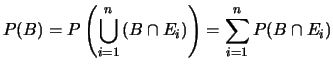 |
(4.6) |
come mostrato anche in figura 4.2, riquadro h).
- Proprietà 3
- :
Se l'evento
 implica l'evento
implica l'evento  , cioè
, cioè
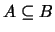 ,
allora
,
allora
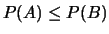 .
In particolare ne segue che
.
In particolare ne segue che
- Proprietà 4
- : probabilità della somma logica nel caso generale:
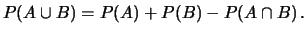 |
(4.7) |
Ne segue che
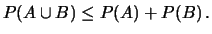 |
(4.8) |
Nel caso di tre eventi la proprietà diventa:
estendibile a  eventi come
eventi come
Questa formula è chiamata
principio di inclusione-esclusione a causa dell'alternanza dei segni.
Queste proprietà sono abbastanza intuitive e si possono dimostrare
facilmente utilizzando i diagrammi di Venn. La 4, in particolare,
è molto importante e, nella soluzione dei problemi, dovrebbe
essere presa in considerazione prima della Regola 3, che può essere
vista come suo sottocaso valido quando
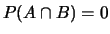 .
Il motivo per cui si sottrae
.
Il motivo per cui si sottrae
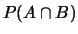 a
a
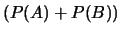 è dovuto al fatto
che, per dirlo alla buona, altrimenti l'elemento
è dovuto al fatto
che, per dirlo alla buona, altrimenti l'elemento
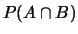 verrebbe contato due volte. Si può vedere in un semplice caso
legato al gioco delle carte:
verrebbe contato due volte. Si può vedere in un semplice caso
legato al gioco delle carte:
- -
- Si consideri un mazzo di carte da gioco italiane con 4 semi e 10 valori
per seme. Si vuole calcolare la
probabilità di estrarre una Coppe (
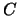 ) o un Asso (
) o un Asso ( ). Supponendo
l'equiprobabilità (carte ben mischiate),
le probabilità
di una Coppe o di un Asso sono rispettivamente
). Supponendo
l'equiprobabilità (carte ben mischiate),
le probabilità
di una Coppe o di un Asso sono rispettivamente
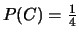 ,
,
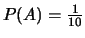 . È chiaro che se si
sommano semplicemente queste probabilità l'Asso di Coppe viene
contato due volte ed è per questo che bisogna sottrarre dalla
somma la sua probabilità (
. È chiaro che se si
sommano semplicemente queste probabilità l'Asso di Coppe viene
contato due volte ed è per questo che bisogna sottrarre dalla
somma la sua probabilità (
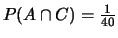 ),
ottenendo come risultato
),
ottenendo come risultato
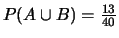 .
.
Subsections




Next: pzd100Dimostrazioni delle proprietà della
Up: Regole della probabilità
Previous: Evento condizionato
Indice
Giulio D'Agostini
2001-04-02