Chiariamo ora meglio il concetto di evento condizionato.
![]() è una qualsiasi affermazione rispetto alla quale siamo in
stato di incertezza, ma che può essere vera o falsa nell'ipotesi
che
è una qualsiasi affermazione rispetto alla quale siamo in
stato di incertezza, ma che può essere vera o falsa nell'ipotesi
che ![]() sia vera. Nell'ipotesi che
sia vera. Nell'ipotesi che ![]() sia falsa
l'evento
sia falsa
l'evento ![]() perde di significato.
Può essere schematizzata quindi con:
perde di significato.
Può essere schematizzata quindi con:
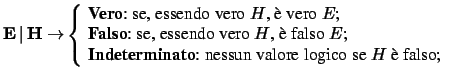 |
(4.3) |
Bisogna fare attenzione a non confondere ![]() e
e ![]() .
Consideriamo l'esempio del lancio dei due dadi di figura 4.1.
Prendiamo l'evento
condizionato ``6 al secondo dado condizionato dal verificarsi di 6 al primo
dado''. Sebbene dal punto di vista geometrico, considerando il verificarsi
del doppio 6,
.
Consideriamo l'esempio del lancio dei due dadi di figura 4.1.
Prendiamo l'evento
condizionato ``6 al secondo dado condizionato dal verificarsi di 6 al primo
dado''. Sebbene dal punto di vista geometrico, considerando il verificarsi
del doppio 6, ![]() e
e ![]() sembrerebbero la stessa cosa, cambia l'ambiente
entro cui tale evento è considerato. Infatti
sembrerebbero la stessa cosa, cambia l'ambiente
entro cui tale evento è considerato. Infatti
![]() è l'intersezione di
è l'intersezione di ![]() e di
e di ![]() riferita allo spazio campionario
riferita allo spazio campionario ![]() costituito
dalle 36 possibilità, mentre
costituito
dalle 36 possibilità, mentre ![]() è sempre l'intersezione dei
due, ma riferita allo spazio campionario ridotto
è sempre l'intersezione dei
due, ma riferita allo spazio campionario ridotto ![]() costituito da
costituito da ![]() .
.
Quindi, anche se ![]() e
e ![]() sono veri
simultaneamente (diciamo che sono ``uguali dal punto di vista fisico''),
essi differiscono quando siamo in condizione di incertezza,
in quanto siamo interessati al verificarsi di
sono veri
simultaneamente (diciamo che sono ``uguali dal punto di vista fisico''),
essi differiscono quando siamo in condizione di incertezza,
in quanto siamo interessati al verificarsi di ![]() solo nell'ipotesi
che
solo nell'ipotesi
che ![]() sia vero. Ciò
si riflette sulla valutazione della probabilità.
In particolare si intuisce come
sia vero. Ciò
si riflette sulla valutazione della probabilità.
In particolare si intuisce come
![]() sia maggiore o uguale a
sia maggiore o uguale a
![]() ,
in quanto l'evento è contemplato
all'interno di una classe di ipotesi più ristretta.
,
in quanto l'evento è contemplato
all'interno di una classe di ipotesi più ristretta.
Un caso particolare immediato che mostra la diversa valutazione di probabilità nei due casi è
| (4.4) |