



Next: Teorema di Bayes
Up: Probabilità delle cause e
Previous: Probabilità delle cause e
Indice
Un modo interessante di rileggere la probabilità condizionata
è di pensare il condizionante causa
dell'evento (visto come effetto).
Questo vale, ad esempio, se si considerano gli eventi
condizionati:
- -
- ``sopravvive almeno cinque anni''
 ``ha subito un trapianto al fegato'';
``ha subito un trapianto al fegato'';
- -
- ``auto rubata''
 ``auto nuova e di valore'';
``auto nuova e di valore'';
- -
- ``l'ago della bilancia si posiziona su 1000.00g''
 ``chilogrammo
campione su bilancia
commerciale di laboratorio'';
``chilogrammo
campione su bilancia
commerciale di laboratorio'';
- -
- ``si registrano
 conteggi in un contatore di radioattività''
conteggi in un contatore di radioattività''
 ``la radioattività
ambientale vale
``la radioattività
ambientale vale  '';
'';
- -
- ``si osservano
 globuli bianchi in un piccolo campione di sangue
osservato al microscopio''
globuli bianchi in un piccolo campione di sangue
osservato al microscopio'' ``il sangue contiene
``il sangue contiene  globuli bianchi
per unità di volume''.
globuli bianchi
per unità di volume''.
Il condizionante viene visto come causa
che può provocare
i vari effetti corrispondenti agli eventi
condizionati (vedi figura 5.2):
La causa è da intendersi inoltre in senso lato, come teoria che
può dar luogo a dei fenomeni osservati,
ovvero grandezza fisica responsabile dei valori registrati
dagli strumenti:
ovvero
Nel condizionante sono stati esplicitate anche altre cause
concomitanti che sono ugualmente responsabili degli effetti osservati.
``Condizioni al contorno'' e ``fattori di influenza'' indicano
genericamente tutte le condizioni iniziali o altri fattori esterni
alla teoria, calibrazioni degli strumenti, variabili e disturbi
ambientali, e così via.
Figura:
Deduzione e induzione
 |
Si intuisce che, come indicato nella citazione di Poincaré
posta all'inizio del capitolo,
se si riesce a trovare una regola per invertire la probabilità
e valutare
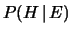 a partire da
a partire da
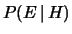 , questa potrà essere
utilizzata come una via per imparare dall'esperienza, alternativa
allo scetticismo di Hume o al falsificazionismo popperiano.
In questo capitolo indicheremo la possibile strada da seguire e
mostreremo che i risultati che si ottengono sono sensati.
Tentare di dimostrare invece la
``certezza'' di questo approccio sarebbe invece
un paradosso autoreferenziale, anche se qualcuno osa dire che
``nei ragionamenti in condizioni di incertezza l'unica cosa che oggigiorno
sembra certa sia come trattare le incertezze''.
, questa potrà essere
utilizzata come una via per imparare dall'esperienza, alternativa
allo scetticismo di Hume o al falsificazionismo popperiano.
In questo capitolo indicheremo la possibile strada da seguire e
mostreremo che i risultati che si ottengono sono sensati.
Tentare di dimostrare invece la
``certezza'' di questo approccio sarebbe invece
un paradosso autoreferenziale, anche se qualcuno osa dire che
``nei ragionamenti in condizioni di incertezza l'unica cosa che oggigiorno
sembra certa sia come trattare le incertezze''.
Prima di proseguire è importante aggiungere due note, per evitare
che la visione causa-effetto stravolga il concetto più generale
- conoscitivo - della probabilità condizionata.
Innanzitutto ricordiamo che la probabilità
condizionata
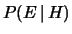 è da intendersi
come probabilità di
è da intendersi
come probabilità di  nell'ipotesi che
nell'ipotesi che 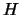 sia vera.
Quindi non va intesa come se fosse calcolabile soltanto dopo che
sia vera.
Quindi non va intesa come se fosse calcolabile soltanto dopo che
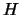 risulta essere vera.
In secondo luogo, l'evento condizionante è da intendersi come uno
stato di informazione e non deve essere vista in funzione strettamente
causale. Questo risulterà chiaro fra poco, quando, nell'inversione
di probabilità l'evento che consideriamo effetto giocherà
il ruolo di condizionante rispetto alla conoscenza sulla ``causa fisica''.
risulta essere vera.
In secondo luogo, l'evento condizionante è da intendersi come uno
stato di informazione e non deve essere vista in funzione strettamente
causale. Questo risulterà chiaro fra poco, quando, nell'inversione
di probabilità l'evento che consideriamo effetto giocherà
il ruolo di condizionante rispetto alla conoscenza sulla ``causa fisica''.
Figura:
Schema di inversione della probabilità
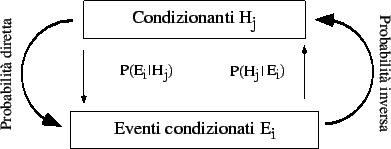 |




Next: Teorema di Bayes
Up: Probabilità delle cause e
Previous: Probabilità delle cause e
Indice
Giulio D'Agostini
2001-04-02
![]() è da intendersi
come probabilità di
è da intendersi
come probabilità di ![]() nell'ipotesi che
nell'ipotesi che ![]() sia vera.
Quindi non va intesa come se fosse calcolabile soltanto dopo che
sia vera.
Quindi non va intesa come se fosse calcolabile soltanto dopo che
![]() risulta essere vera.
In secondo luogo, l'evento condizionante è da intendersi come uno
stato di informazione e non deve essere vista in funzione strettamente
causale. Questo risulterà chiaro fra poco, quando, nell'inversione
di probabilità l'evento che consideriamo effetto giocherà
il ruolo di condizionante rispetto alla conoscenza sulla ``causa fisica''.
risulta essere vera.
In secondo luogo, l'evento condizionante è da intendersi come uno
stato di informazione e non deve essere vista in funzione strettamente
causale. Questo risulterà chiaro fra poco, quando, nell'inversione
di probabilità l'evento che consideriamo effetto giocherà
il ruolo di condizionante rispetto alla conoscenza sulla ``causa fisica''.