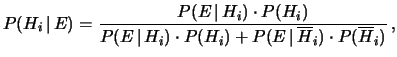Next: Chiavi di lettura del
Up: Probabilità delle cause e
Previous: Inferenza probabilistica
Indice
Consideriamo un evento  e una classe completa di ipotesi
e una classe completa di ipotesi 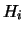 ,
ovvero - ricordiamo - che siano
esaustive e mutuamente esclusive:
,
ovvero - ricordiamo - che siano
esaustive e mutuamente esclusive:
Applicando la formula della probabilità composta si ottiene
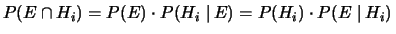 |
(5.2) |
da cui segue
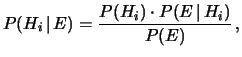 |
(5.3) |
ovvero
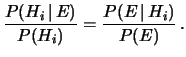 |
(5.4) |
(Per la validità di queste due equazioni non è necessaria
la condizione che le ipotesi 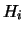 formino una classe completa.)
formino una classe completa.)
Figura:
Decomposizione di un evento nell'unione dei
prodotti logici con gli elementi di una partizione finita 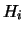 .
.
 |
Utilizzando la formula di disintegrazione della probabilità
(4.26), valida sotto ipotesi di classe completa
degli 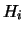 (e che riportiamo per comodità
insieme alla figura 5.3 della decomposizione dell'evento
(e che riportiamo per comodità
insieme alla figura 5.3 della decomposizione dell'evento
 da cui la (4.26) discende)
si ottiene:
da cui la (4.26) discende)
si ottiene:
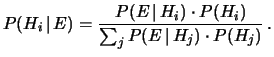 |
(5.5) |
Questa è la forma standard con cui è conosciuto il
teorema di Bayes,
sebbene (5.3) e (5.4) siano modi alternativi
di scriverlo.
Se si osserva che il denominatore non è altro che un fattore
di normalizzazione, ossia tale che
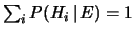 ,
la formula (5.5) può essere più facilmente
memorizzata come
,
la formula (5.5) può essere più facilmente
memorizzata come
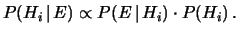 |
(5.6) |
Inoltre, fattorizzando 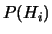 al secondo membro della (5.5)
e ricordando che in realtà le probabilità sono
sempre da intendersi condizionate da una ipotesi implicita
che qui
indichiamo
con
al secondo membro della (5.5)
e ricordando che in realtà le probabilità sono
sempre da intendersi condizionate da una ipotesi implicita
che qui
indichiamo
con 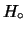 , possiamo riscrivere
la formula (5.5)
come5.1
, possiamo riscrivere
la formula (5.5)
come5.1
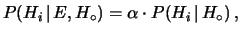 |
(5.10) |
con
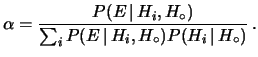 |
(5.11) |
Se si considera la sola ipotesi 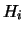 e
la sua opposta
e
la sua opposta
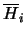 la (5.5) si riduce a
la (5.5) si riduce a
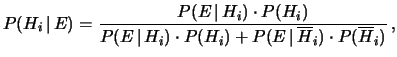 |
(5.12) |
da cui è possibile riscrivere
il teorema di Bayes ancora in un'altra forma:
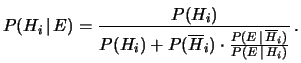 |
(5.13) |
Un'ultima forma, molto conveniente perché lega due qualsiasi
ipotesi 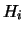 e
e 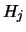 incompatibili (anche se non formano una classe completa)
è
incompatibili (anche se non formano una classe completa)
è
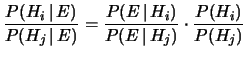 |
(5.14) |
Questi diversi modi di scrivere essenzialmente la stessa
formula riflettono l'importanza di questo semplice
teorema.




Next: Chiavi di lettura del
Up: Probabilità delle cause e
Previous: Inferenza probabilistica
Indice
Giulio D'Agostini
2001-04-02
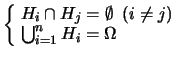
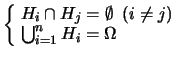

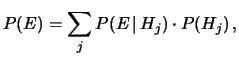
![]() ,
la formula (5.5) può essere più facilmente
memorizzata come
,
la formula (5.5) può essere più facilmente
memorizzata come
![]() al secondo membro della (5.5)
e ricordando che in realtà le probabilità sono
sempre da intendersi condizionate da una ipotesi implicita
che qui
indichiamo
con
al secondo membro della (5.5)
e ricordando che in realtà le probabilità sono
sempre da intendersi condizionate da una ipotesi implicita
che qui
indichiamo
con ![]() , possiamo riscrivere
la formula (5.5)
come5.1
, possiamo riscrivere
la formula (5.5)
come5.1
![]() e
la sua opposta
e
la sua opposta
![]() la (5.5) si riduce a
la (5.5) si riduce a