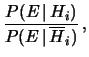Ad esempio, se stimo che la probabilità che una squadra di calcio vinca un incontro raddoppi qualora venissi a sapere che nel primo tempo è in vantaggio, ne segue che, se so che la squadra ha vinto l'incontro, la probabilità che essa fosse già in vantaggio al primo tempo diventa il doppio di quanto non l'avessi valutata precedentemente.è modificata dall'ipotesi che
sia vera dello stesso fattore dell quale
è modificata dall'ipotesi che
sia vera.
la probabilità didato
è proporzionale alla probabilità di
per la probabilità di
dato
.
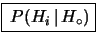
- (anche indicata come
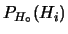 o, ancora più succintamente, come
o, ancora più succintamente, come
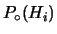 )
è la probabilità iniziale, o a priori,
ovvero la probabilità di
)
è la probabilità iniziale, o a priori,
ovvero la probabilità di 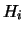 condizionata da tutte le
ipotesi preliminari
condizionata da tutte le
ipotesi preliminari 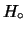 , con esclusione del verificarsi o meno
di
, con esclusione del verificarsi o meno
di  ;
;
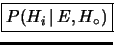
- (o semplicemente
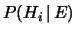 )
è la probabilitità finale, o a posteriori:
è la probabilità
di
)
è la probabilitità finale, o a posteriori:
è la probabilità
di 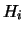 riaggiornata alla luce dell'ipotesi che
riaggiornata alla luce dell'ipotesi che  sia vero;
sia vero;
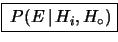
- (o semplicemente
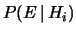 )
è la verosimiglianza, ovvero una misura di quanto è verosimile
)
è la verosimiglianza, ovvero una misura di quanto è verosimile
 alla luce di
alla luce di 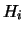 (o, in termini di causa ed effetto, di quanto
facilmente
(o, in termini di causa ed effetto, di quanto
facilmente 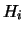 possa produrre
possa produrre  ).
Si noti come anche la verosimiglianza sia
valutata subordinatamente allo stato di conoscenza
).
Si noti come anche la verosimiglianza sia
valutata subordinatamente allo stato di conoscenza 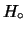 .
.
il rapporto delle probabilità viene modificato dal rapporto delle verosimiglianze
denominato fattore di Bayes.Questo modo di vedere il teorema è molto pratico quando non ha interesse, o non è pratico, considerare tutte le ipotesi che formano una classe completa. Ad esempio nella ricerca scientifica non ha senso chiedersi la probabilità assoluta di una teoria, ma ha soltanto senso valutarne la credibilità rispetto ad una o più concorrenti. Quindi dalla (5.14) è possibile calcolarsi5.2
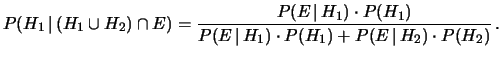 |
(5.16) |