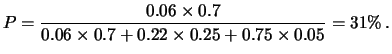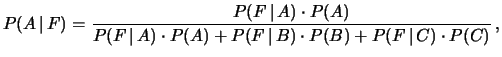Next: Esempi tipici di applicazione
Up: Probabilità delle cause e
Previous: Chiavi di lettura del
Indice
Includiamo un esempio in cui si mostra come arrivare alla formula
di Bayes da considerazioni combinatorie, ad uso di coloro
che si trovano più a loro agio con esempi di questo tipo.
Si tenga conto che tale visione è comunque fortemente limitativa
in quanto non è di uso generale e, in particolare, non
è utilizzabile nella valutazione della probabilità delle cause
e quindi in tutti i casi di inferenza legata alle misure.
Supponiamo che il mercato delle automobili
sia costituito da tre sole fabbriche A, B e C, le
quali
detengono rispettivamente le seguenti quote di mercato: 70%,
25% e 5%. Supponiamo inoltre di sapere che dopo dieci anni siano
ancora funzionanti: il 6% delle auto A, il 22% delle B e
il 75% delle C. Un amico ci dice di avere un'auto di oltre 10 anni.
Qual'è la probabilità che sia una A?
Un modo di risolvere il problema è di considerare il
numero di auto prodotte e quello di quelle
circolanti dopo dieci anni, come schematizzato nella
seguente tabella:
| Marca |
Quota |
P(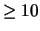 anni) anni) |
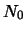 |
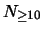 |
| A |
70% |
6% |
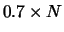 |
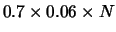 |
| B |
25% |
22% |
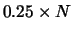 |
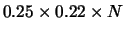 |
| C |
5% |
75% |
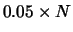 |
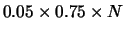 |
Troviamo quindi che la probabilità cercata è:
Interpretando le varie frazioni come probabilità (nel senso
di usare la valutazione di probabilità dai casi favorevoli e
quelli possibili), possiamo
riscrivere questo risultato come
dove 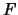 sta per ``funziona dopo 10 anni''. Si riconosce in questa
formula particolare la (5.5).
sta per ``funziona dopo 10 anni''. Si riconosce in questa
formula particolare la (5.5).




Next: Esempi tipici di applicazione
Up: Probabilità delle cause e
Previous: Chiavi di lettura del
Indice
Giulio D'Agostini
2001-04-02