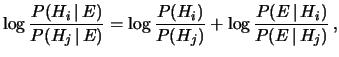Next: Indifferenza iniziale e massima
Up: Probabilità delle cause e
Previous: Osservazioni indipendenti e prodotto
Indice
Se si parte da una situazione iniziale di incertezza
su due ipotesi 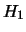 e
e 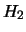 , l'osservazione di una successione
di eventi {
, l'osservazione di una successione
di eventi {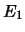 ,
, 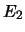 ,
, 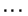 ,
, 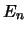 }
altera le probabilità relative
ma non può mai arrivare a conclusione certe fintanto
le verosimiglianze
}
altera le probabilità relative
ma non può mai arrivare a conclusione certe fintanto
le verosimiglianze
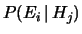 sono diverse da zero. Può
accadere invece che gli eventi osservati favoriscano fortemente
una delle due ipotesi e quindi che, ad esempio,
dopo un certo numero di eventi,
sono diverse da zero. Può
accadere invece che gli eventi osservati favoriscano fortemente
una delle due ipotesi e quindi che, ad esempio,
dopo un certo numero di eventi,
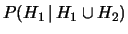 sia molto prossima
a 0. Sebbene il valore di zero non sia mai raggiunto è chiaro che
0.1 è ben diverso da 0.001 o da
sia molto prossima
a 0. Sebbene il valore di zero non sia mai raggiunto è chiaro che
0.1 è ben diverso da 0.001 o da 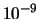 . Quando le probabilità
sono molto piccole quello che interessa veramente è l'ordine di
grandezza e quindi sembrerebbe naturale considerarne il logaritmo.
Ma questo non funziona per le probabilità molto prossime a 1.
Il rapporto delle probabilità è invece un numero compreso fra
0 e infinito che meglio si presta ad essere trattato con i logaritmi,
in quanto
. Quando le probabilità
sono molto piccole quello che interessa veramente è l'ordine di
grandezza e quindi sembrerebbe naturale considerarne il logaritmo.
Ma questo non funziona per le probabilità molto prossime a 1.
Il rapporto delle probabilità è invece un numero compreso fra
0 e infinito che meglio si presta ad essere trattato con i logaritmi,
in quanto
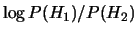 va da meno infinito a più infinito
e vale 0 quando
va da meno infinito a più infinito
e vale 0 quando
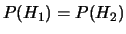 .
.
Applicando questa idea alla (5.14)
si ottiene
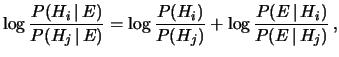 |
(5.24) |
Ossia il logaritmo dei rapporti di
credibilità
di due eventi è
modificato da incrementi pari al logaritmo del fattore di Bayes.
Se sono stati osservati  eventi indipendenti si ha
eventi indipendenti si ha




Next: Indifferenza iniziale e massima
Up: Probabilità delle cause e
Previous: Osservazioni indipendenti e prodotto
Indice
Giulio D'Agostini
2001-04-02