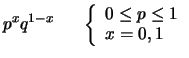Processo di Bernoulli

Next: Combinazione di molti processi Up: Distribuzioni elementari notevoli Previous: pzd100Distribuzione uniforme discreta - Indice

Processo di Bernoulli

Possiamo pensare al valore di verità di un evento, definito come 1 se è vero e 0 se è falso, come una variabile casuale (nel paragrafo 2.17 avevamo introdotto a tale scopo l'indicatore dell'evento 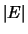$\vert E\vert$ ).

**Figura:** Distribuzione di Bernoulli per 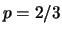e .
$\begin{figure}\centering\epsfig{file=fig/dago67.eps,clip=,width=0.5\linewidth}\end{figure}$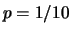

La distribuzione che ne segue è molto semplice, ma essa è di grande importanza perché illustra una schematizzazione che descrive molti casi di interesse, come vedremo fra breve. Per questa ragione tale schematizzazione è nota sotto nome proprio: si parla di processo di Bernoulli. A partire da tanti processi ``elementari'' di questo tipo si possono costruire altre distribuzioni largamente usate.

Schematizzando, il processo di Bernoulli consiste nell'effettuare una prova nella quale

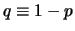si valuta in la probabilità di un certo evento, chiamato convenzionalmente successo; di consequenza, $q\equiv 1-p$ è la probabilità di insuccesso; il ruolo di successo e insuccesso sono assolutamente arbitrari e quindi tutti i ragionamenti saranno simmetrici; è però importante fare attenzione alla convenzione utilizzata;
la variabile assume il valore 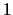se l'evento si verifica e 0 se esso non si verifica.

Ne segue che

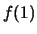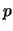$\displaystyle f(1)$	$\displaystyle =$	$\displaystyle p$	(6.16)
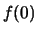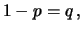$\displaystyle f(0)$	$\displaystyle =$	$\displaystyle 1-p = q \,,$	(6.17)
o, in generale, $\displaystyle \hspace{2.0 cm}$
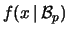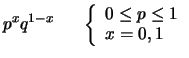$\displaystyle f(x\,\vert\,{\cal B}_p)$	$\displaystyle =$	$\displaystyle p^xq^{1-x}\hspace{.6 cm} \left\{ \begin{array}{l} 0 \le p \le 1 \\ x=0, 1 \end{array}\right.$	(6.18)

Next: Combinazione di molti processi Up: Distribuzioni elementari notevoli Previous: pzd100Distribuzione uniforme discreta - Indice

Giulio D'Agostini 2001-04-02