



Next: Distribuzione geometrica
Up: Distribuzioni elementari notevoli
Previous: Processo di Bernoulli
Indice
Combinazione di molti processi di Bernoulli indipendenti
e di uguale probabilità
Molto spesso si è interessati a eventi ``dello stesso
tipo''6.7,
ai quali assegnamo la stessa probabilità e che consideriamo
stocasticamente indipendenti, ad esempio
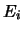 = ``testa all'
= ``testa all'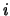 -mo lancio di una moneta''
(o, equivalentemente, ``...per l'
-mo lancio di una moneta''
(o, equivalentemente, ``...per l'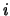 -ma moneta numerata'').
-ma moneta numerata'').
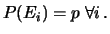 |
(6.19) |
Considerando
processi di Bernoulli indipendenti, si può essere
interessati a due domande tipiche:
- quante prove bisogna effettuare affinché si verifichi per la prima
volta un successo? (Più esattamente: ``quanto vale la probabilità che
il successo si verifichi per la prima volta alla prova
 ?'')
?'')
- se si effettuano
 prove, quanto vale la probabilità che si verifichino
prove, quanto vale la probabilità che si verifichino
 successi?
successi?
Le due schematizzazioni corrispondono rispettivamente alle cosiddette
distribuzioni geometrica e binomiale.
Un altro problema che può avere un certo interesse, ma di minore
rilevanza rispetto agli altri per le applicazioni che presenteremo
in questo testo, è:
- 3.
- quanto vale la probabilità che il
 -mo successo si verifichi
esattamente alla prova
-mo successo si verifichi
esattamente alla prova  ?
?
Ad esso è associata la distribuzione di Pascal
e, in modo complementare, la binomiale negativa.




Next: Distribuzione geometrica
Up: Distribuzioni elementari notevoli
Previous: Processo di Bernoulli
Indice
Giulio D'Agostini
2001-04-02