Is there a signal?

Next: Signal and background: a Up: Poisson model: dependence on Previous: Including systematic effects Contents

Is there a signal?

There is an important remark to be made on the interpretation of the result: can we conclude from an upper limit that the searched for signal does not exist? Tacitly yes. But let us take the final distribution of $\lambda$ for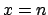

(with a uniform prior and neglecting systematic effects) and let us read the result in a complementary way:

$\displaystyle P(\lambda\ge \lambda_L) = e^{-\lambda_L}\,.$

We obtain, for example:

$\displaystyle P(\lambda\ge 10^{-1})$	$\displaystyle =$	$\displaystyle 90\%$
$\displaystyle P(\lambda\ge 10^{-2})$	$\displaystyle =$	$\displaystyle 99\%$
$\displaystyle \ldots$		$\displaystyle \ldots$

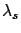Since $P(\lambda =0)=0$ , it seems that we are almost sure that there is a signal, although of very small size. The solution to this apparent paradox is to remember that the analysis was done assuming that a new signal existed and that we only wanted to infer its size from the observation, under this assumption. On the other hand, from the experimental result we cannot conclude that the signal does not exist.

For the purpose of these notes, we follow the good sense of physicists who, for reasons of economy and simplicity, tend not to believe in a new signal until there is strong evidence that it exists. However, to state with a number what `strong evidence' means is rather subjective. For a more extensive discussion about this point see Ref. [25].

Next: Signal and background: a Up: Poisson model: dependence on Previous: Including systematic effects Contents

Giulio D'Agostini 2003-05-15