



Next: Bayesian inference and maximum
Up: Statistical inference
Previous: Statistical inference
Contents
Bayesian inference
In the Bayesian framework the inference
is performed by calculating
the final distribution of the random variable
associated with the true
values of the physical quantities
from all available information.
Let us call
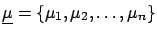 the n-tuple (``vector'') of observables,
the n-tuple (``vector'') of observables,
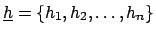 the n-tuple
of the true
values of the physical quantities of interest,
and
the n-tuple
of the true
values of the physical quantities of interest,
and
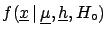 the n-tuple of all the
possible realizations of the influence variables
the n-tuple of all the
possible realizations of the influence variables 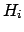 .
The term ``influence variable'' is used here with
an extended meaning, to indicate not only external factors which
could influence the result (temperature, atmospheric pressure,
and so on) but also any possible calibration constant and any
source of systematic errors.
In fact the distinction between
.
The term ``influence variable'' is used here with
an extended meaning, to indicate not only external factors which
could influence the result (temperature, atmospheric pressure,
and so on) but also any possible calibration constant and any
source of systematic errors.
In fact the distinction between
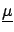 and
and
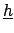 is artificial, since they are all conditional
hypotheses. We separate them simply because at the end we will
``marginalize'' the final joint distribution functions
with respect to
is artificial, since they are all conditional
hypotheses. We separate them simply because at the end we will
``marginalize'' the final joint distribution functions
with respect to
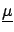 , integrating the joint distribution
with respect to the other hypotheses
considered as influence variables.
, integrating the joint distribution
with respect to the other hypotheses
considered as influence variables.
The likelihood of the sample
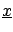 being
produced from
being
produced from
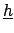 and
and
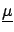 and the
initial probability are
and the
initial probability are
and
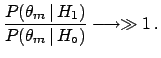 |
(5.1) |
respectively.
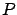 is intended to remind us, yet again, that
likelihoods and priors
-- and hence conclusions -- depend
on all explicit and implicit assumptions within the problem,
and in particular on the parametric functions used to
model priors and likelihoods.
To simplify the formulae,
is intended to remind us, yet again, that
likelihoods and priors
-- and hence conclusions -- depend
on all explicit and implicit assumptions within the problem,
and in particular on the parametric functions used to
model priors and likelihoods.
To simplify the formulae, 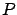 will no longer be written explicitly.
will no longer be written explicitly.
Using the Bayes formula for multidimensional continuous
distributions [an extension of ( ![[*]](file:/usr/lib/latex2html/icons/crossref.png) )]
we obtain the most general formula
of inference,
)]
we obtain the most general formula
of inference,
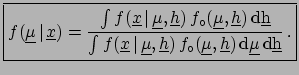 |
(5.2) |
yielding the joint distribution of all conditional variables
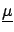 and
and
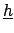 which are responsible
for the observed sample
which are responsible
for the observed sample
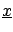 .
To obtain the final distribution of
.
To obtain the final distribution of
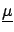 one has to integrate (
one has to integrate (![[*]](file:/usr/lib/latex2html/icons/crossref.png) )
over all possible values of
)
over all possible values of
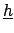 ,
obtaining
,
obtaining
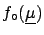 |
(5.3) |
Apart from the technical problem of evaluating the integrals,
if need be
numerically or using Monte Carlo
methods5.1,
(![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) represents the most general form
of hypothetical inductive inference.
The word ``hypothetical''
reminds us of
) represents the most general form
of hypothetical inductive inference.
The word ``hypothetical''
reminds us of 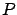 .
.
When all the sources of influence are under control,
i.e. they can be assumed to take a precise value,
the initial distribution can be factorized by a
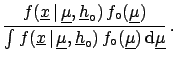 and a Dirac
and a Dirac
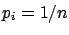 ,
obtaining the much simpler formula
,
obtaining the much simpler formula
Even if formulae (![[*]](file:/usr/lib/latex2html/icons/crossref.png) )-(
)-(![[*]](file:/usr/lib/latex2html/icons/crossref.png) )
look complicated because of the
multidimensional integration and of the continuous nature
of
)
look complicated because of the
multidimensional integration and of the continuous nature
of
 , conceptually they are
identical to the example
of the
, conceptually they are
identical to the example
of the
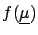 measurement discussed in Section
measurement discussed in Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.
The final probability density function provides the
most complete and detailed information about the
unknown quantities, but sometimes (almost always  ) one
is not interested in
full knowledge of
) one
is not interested in
full knowledge of
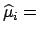 , but just in a
few numbers which summarize at best the position and the width
of the distribution (for example when publishing the result
in a journal in the most compact way).
The most natural quantities for this purpose
are the expectation value and the variance, or the standard deviation.
Then the Bayesian best estimate of a physical quantity
is:
, but just in a
few numbers which summarize at best the position and the width
of the distribution (for example when publishing the result
in a journal in the most compact way).
The most natural quantities for this purpose
are the expectation value and the variance, or the standard deviation.
Then the Bayesian best estimate of a physical quantity
is:
When many true values are inferred
from the same data
the numbers which synthesize the result are not
only the expectation values and variances, but also the covariances,
which give at least the
correlation coefficients between the variables:
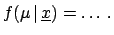 |
(5.7) |
In the following sections we will deal in most cases
with only one value to infer:
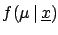 |
(5.8) |




Next: Bayesian inference and maximum
Up: Statistical inference
Previous: Statistical inference
Contents
Giulio D'Agostini
2003-05-15
![]() being
produced from
being
produced from
![]() and
and
![]() and the
initial probability are
and the
initial probability are
![]() )]
we obtain the most general formula
of inference,
)]
we obtain the most general formula
of inference,
![]() and a Dirac
and a Dirac
![]() ,
obtaining the much simpler formula
,
obtaining the much simpler formula
![]() ) one
is not interested in
full knowledge of
) one
is not interested in
full knowledge of
![]() , but just in a
few numbers which summarize at best the position and the width
of the distribution (for example when publishing the result
in a journal in the most compact way).
The most natural quantities for this purpose
are the expectation value and the variance, or the standard deviation.
Then the Bayesian best estimate of a physical quantity
is:
, but just in a
few numbers which summarize at best the position and the width
of the distribution (for example when publishing the result
in a journal in the most compact way).
The most natural quantities for this purpose
are the expectation value and the variance, or the standard deviation.
Then the Bayesian best estimate of a physical quantity
is: