



Next: Correction for known systematic
Up: Uncertainty due to systematic
Previous: Uncertainty due to systematic
Contents
Example: uncertainty of the instrument scale
offset
In our scheme any quantity of influence of which we do not know the exact
value is a source of systematic error. It will change the final
distribution of 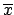 and hence its uncertainty.
We have already discussed the most general case in Section
and hence its uncertainty.
We have already discussed the most general case in Section
![[*]](file:/usr/lib/latex2html/icons/crossref.png) . Let us make a simple
application making a small variation to the example in Section
. Let us make a simple
application making a small variation to the example in Section
![[*]](file:/usr/lib/latex2html/icons/crossref.png) : the ``zero'' of the instrument
is not known exactly, owing to calibration uncertainty.
This can be parametrized assuming that its true value
: the ``zero'' of the instrument
is not known exactly, owing to calibration uncertainty.
This can be parametrized assuming that its true value
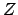 is normally distributed around 0 (i.e. the calibration
was properly done!) with a standard deviation
is normally distributed around 0 (i.e. the calibration
was properly done!) with a standard deviation 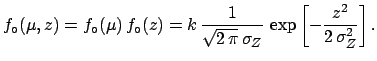 .
Since, most probably, the true value of
.
Since, most probably, the true value of 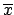 is independent of
the true value of
is independent of
the true value of 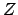 , the initial joint probability density
function can be written as the product of the marginal ones:
, the initial joint probability density
function can be written as the product of the marginal ones:
![$\displaystyle f_\circ(\mu,z)=f_\circ(\mu)\,f_\circ(z)= k\,\frac{1}{\sqrt{2\,\pi}\,\sigma_Z} \,\exp{\left[-\frac{z^2}{2\,\sigma_Z^2}\right]}\,.$](img828.png) |
(5.66) |
Also the likelihood changes with respect to
(![[*]](file:/usr/lib/latex2html/icons/crossref.png) ):
):
![$\displaystyle f(x_1\,\vert\,\mu,z) = \frac{1}{\sqrt{2\,\pi}\,\sigma_1} \,\exp{\left[-\frac{(x_1-\mu-z)^2}{2\,\sigma_1^2}\right]}\,.$](img829.png) |
(5.67) |
Putting all the pieces together and making use of
(![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) we finally get
) we finally get
Integrating5.8we get
![$\displaystyle f(\mu) = f(\mu\,\vert\,x_1, \ldots,f_\circ(z)) = \frac{1}{\sqrt{2...
...a_Z^2}} \,\exp{\left[-\frac{(\mu-x_1)^2}{2\,(\sigma_1^2+\sigma_Z^2)}\right]}\,.$](img832.png) |
(5.68) |
The result is that 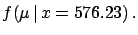 is still a Gaussian, but with
a larger variance. The global standard uncertainty
is the quadratic combination of
that due to the statistical fluctuation of the data sample
and the uncertainty due to the imperfect knowledge of the
systematic effect:
is still a Gaussian, but with
a larger variance. The global standard uncertainty
is the quadratic combination of
that due to the statistical fluctuation of the data sample
and the uncertainty due to the imperfect knowledge of the
systematic effect:
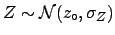 |
(5.69) |
This result is well known, although there are still
some ``old-fashioned'' recipes which require
different combinations
of the contributions to be performed.
It must be noted that in this framework it makes no sense
to speak of ``statistical'' and ``systematical'' uncertainties,
as if they were of a different nature.
They have the same probabilistic nature:
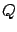 is around
is around 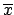 with a standard deviation
with a standard deviation
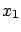 , and
, and 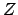 is around 0 with standard deviation
is around 0 with standard deviation 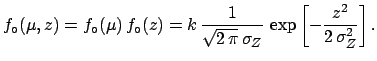 .
What distinguishes the two components
is how the knowledge of the uncertainty is gained: in one case
(
.
What distinguishes the two components
is how the knowledge of the uncertainty is gained: in one case
(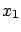 ) from repeated measurements; in the second case (
) from repeated measurements; in the second case (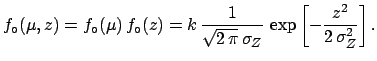 )
the evaluation was done by somebody else (the constructor
of the instrument),
or in a previous experiment, or guessed from the knowledge of the
detector, or by simulation, etc. This is the reason why the ISO
Guide[3] prefers the generic names Type A and Type B
for the two kinds of contribution to global
uncertainty. In particular,
the name ``systematic uncertainty'' should be avoided, while
it is correct to speak about ``uncertainty due to a systematic effect''.
)
the evaluation was done by somebody else (the constructor
of the instrument),
or in a previous experiment, or guessed from the knowledge of the
detector, or by simulation, etc. This is the reason why the ISO
Guide[3] prefers the generic names Type A and Type B
for the two kinds of contribution to global
uncertainty. In particular,
the name ``systematic uncertainty'' should be avoided, while
it is correct to speak about ``uncertainty due to a systematic effect''.




Next: Correction for known systematic
Up: Uncertainty due to systematic
Previous: Uncertainty due to systematic
Contents
Giulio D'Agostini
2003-05-15
![$\displaystyle f_\circ(\mu,z)=f_\circ(\mu)\,f_\circ(z)= k\,\frac{1}{\sqrt{2\,\pi}\,\sigma_Z} \,\exp{\left[-\frac{z^2}{2\,\sigma_Z^2}\right]}\,.$](img828.png)
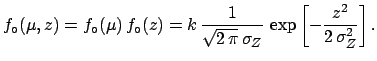 .
Since, most probably, the true value of
.
Since, most probably, the true value of ![$\displaystyle f_\circ(\mu,z)=f_\circ(\mu)\,f_\circ(z)= k\,\frac{1}{\sqrt{2\,\pi}\,\sigma_Z} \,\exp{\left[-\frac{z^2}{2\,\sigma_Z^2}\right]}\,.$](img828.png)
![$\displaystyle f(x_1\,\vert\,\mu,z) = \frac{1}{\sqrt{2\,\pi}\,\sigma_1} \,\exp{\left[-\frac{(x_1-\mu-z)^2}{2\,\sigma_1^2}\right]}\,.$](img829.png)
![$\displaystyle f(\mu\,\vert\,x_1, \ldots,f_\circ(z)) = \frac{ \int \frac{1}{\sqr...
...ma_Z} \exp{\left[-\frac{z^2}{2\,\sigma_Z^2}\right]} \,\rm {d}\mu\,\rm {d}z }\,.$](img830.png)
![]() is around
is around ![]() with a standard deviation
with a standard deviation
![]() , and
, and ![]() is around 0 with standard deviation
is around 0 with standard deviation 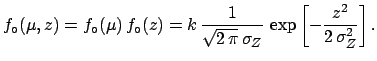 .
What distinguishes the two components
is how the knowledge of the uncertainty is gained: in one case
(
.
What distinguishes the two components
is how the knowledge of the uncertainty is gained: in one case
(![]() ) from repeated measurements; in the second case (
) from repeated measurements; in the second case (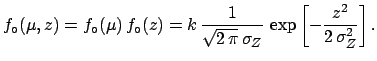 )
the evaluation was done by somebody else (the constructor
of the instrument),
or in a previous experiment, or guessed from the knowledge of the
detector, or by simulation, etc. This is the reason why the ISO
Guide[3] prefers the generic names Type A and Type B
for the two kinds of contribution to global
uncertainty. In particular,
the name ``systematic uncertainty'' should be avoided, while
it is correct to speak about ``uncertainty due to a systematic effect''.
)
the evaluation was done by somebody else (the constructor
of the instrument),
or in a previous experiment, or guessed from the knowledge of the
detector, or by simulation, etc. This is the reason why the ISO
Guide[3] prefers the generic names Type A and Type B
for the two kinds of contribution to global
uncertainty. In particular,
the name ``systematic uncertainty'' should be avoided, while
it is correct to speak about ``uncertainty due to a systematic effect''.