Adding pieces of evidence
Imagine now the following variant of the previous toy
experiment. After the white ball is observed, you put it again
in the box, shake well and make a second extraction.
You get white the second time too. Calling 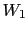 and
and 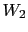 the
two observations,
we have now:11
the
two observations,
we have now:11
that,
using the compact notation introduced above,
we can rewrite in the following enlighting forms.
The first is
[Eq. (14)]
that is,
the final odds after the first inference become the
initial odds of the second inference
(and so on, if there are several pieces of evidence).
Therefore, beginning
from a situation in which 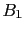 was thirteen times more credible
than
was thirteen times more credible
than 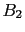 is exactly equivalent to having
started from unitary odds updated
by a factor 13 due to a piece of evidence.
is exactly equivalent to having
started from unitary odds updated
by a factor 13 due to a piece of evidence.
The second form comes from Eq. (13):
i.e.12
Bayes factors due to
independent13pieces of evidence multiply. That is,
two independent pieces of evidence (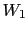 and
and 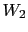 ) are equivalent
to a single piece of evidence (`
) are equivalent
to a single piece of evidence (`
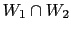 '), whose Bayes factor
is the product of the individual ones.
In our case
'), whose Bayes factor
is the product of the individual ones.
In our case
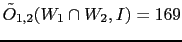 .
.
In general, if we have several hypotheses 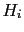 and
several independent
pieces of evidence,
and
several independent
pieces of evidence, 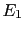 ,
, 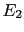 , ...,
, ..., 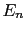 ,
indicated all together as
,
indicated all together as
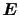 ,
then
Eq. (4) becomes
,
then
Eq. (4) becomes
i.e.
where 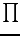 stand for `product'
(analogous to
stand for `product'
(analogous to 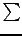 for sums).
for sums).
Giulio D'Agostini
2010-09-30
![]() and
several independent
pieces of evidence,
and
several independent
pieces of evidence, ![]() ,
, ![]() , ...,
, ..., ![]() ,
indicated all together as
,
indicated all together as
![]() ,
then
Eq. (4) becomes
,
then
Eq. (4) becomes