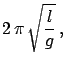 |
(1) |
In order to understand if there is any physical reason behind this
numerical coincidence let us try to understand the property of
Earth that mainly influences the period of the pendulum, and if there
is any simplification due to the fact that the length of the pendulum
is about
![]() of the
meridian.44
The gross value of
of the
meridian.44
The gross value of ![]() depends on mass and
radius45
depends on mass and
radius45 ![]() of the Earth
with local effects due to not exact sphericity
(see Table 4),
mass dishomogeneity and above sea level height.
Moreover, there is a centrifugal term, null at the pole and
maximum at the equator, due to Earth
rotation.46In the
approximation of a perfect sphere, the gravitational acceleration
of the Earth
with local effects due to not exact sphericity
(see Table 4),
mass dishomogeneity and above sea level height.
Moreover, there is a centrifugal term, null at the pole and
maximum at the equator, due to Earth
rotation.46In the
approximation of a perfect sphere, the gravitational acceleration
![]() , i.e. the gravitational force
, i.e. the gravitational force ![]() divided by the mass of the pendulum, is given by
divided by the mass of the pendulum, is given by
| Planet | Physical data [48] | One `meter' pendulum | |||||
| and its period | |||||||
| Mass | Radius |
|
|
|
|
||
| (kg) | (km) |
(g/cm |
(m/s |
(m) | (s) | (s) | |
| Mercury | |
2440 | 5.43 | 3.70 | 0.38 | 1.01 | 58.6 |
| Venus | |
6052 | 5.24 | 8.89 | 0.95 | 1.03 | |
| Earth | |
6378 | 5.52 | 9.80 | 1.00 | 1.00 | 1.00 |
| Mars | |
3397 | 3.93 | 3.69 | 0.53 | 1.19 | 1.03 |
| Jupiter | |
71492 | 1.33 | 23.17 | 11.23 | 2.19 | 0.41 |
| Saturn | |
60268 | 0.69 | 8.98 | 9.47 | 3.23 | 0.45 |
| Uranus | |
25559 | 1.32 | 8.71 | 4.01 | 2.13 | 0.72 |
| Neptune | |
24766 | 1.64 | 11.03 | 3.89 | 1.87 | 0.67 |
| Pluto | |
1137 | 2.06 | 0.66 | 0.19 | 1.64 | |
However, the half period of this pendulum is approximately equal
to the ![]() part of the planet rotation only for Earth
and Mars, which have approximately equal `days'. For all other
planets, the local day can be very different with respect to
the Earth one. In fact,
the rotation speed is related to the initial angular momentum
when the planet was formed and there is no reason why it should
come out to be the same in different planets
(Venus and Pluto are indeed retrograde, i.e. they rotate East-West).
part of the planet rotation only for Earth
and Mars, which have approximately equal `days'. For all other
planets, the local day can be very different with respect to
the Earth one. In fact,
the rotation speed is related to the initial angular momentum
when the planet was formed and there is no reason why it should
come out to be the same in different planets
(Venus and Pluto are indeed retrograde, i.e. they rotate East-West).